Hvad sker der på den anden side af 0? Lær om de negative tal.

Hvad er negative tal?

For at forstå, hvad negative tal eller “minustal” er for en størrelse, er vi nødt til at forstå, at der findes tre forskellige slags tal: de negative, de positive og det neutrale tal. De tal, vi er vant til at kigge på, som 1, 2, 3, 117 og 24, er positive tal.

Det er tal, der er større end 0. De negative tal er de tal, der er modsat de positive tal, altså dem der er mindre end 0. Der er lige så mange negative tal, som der er positive tal, for hvis vi har et negativt tal, kan vi sætte minus foran, og så har vi et negativt tal.

De negative tal hedder altså -1, -2, -3, -117 og -24. De neutrale tal er alle de tal, der hverken er større end eller mindre end 0. Det er der kun et tal, der er: 0!

Tallinjen

Hvis vi skal tegne de negative tal, tegner vi en tallinje. Du har måske før set en tallinje som den her:

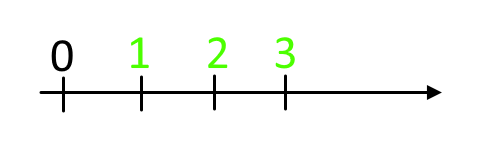
Men den har en side mere, nemlig den negative del. Vi kan udvide den så minustallene også er med:

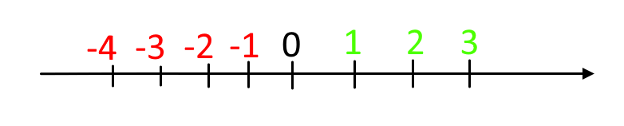
Plus og minus

Nu hvor vi har en tallinje, så kan vi også begynde at regne med de negative tal. Hvis du tænker tilbage på, hvordan du først lærte at plusse, kan du måske huske, at når vi tager et tal og lægger et andet til, så går vi det antal skridt videre på tallinjen. For eksempel, når man tager 4 + 3, starter vi ved 4 og går 3 skridt mod højre. Og fordi vi lander på 7, er 4 + 3 = 7.

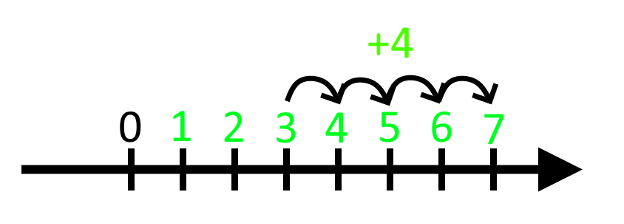
Og det fungerer på samme måde med minus. Hvis vi starter på 7 og trækker 3 fra, så ender vi på 4, og derfor er 7 - 3 = 4.

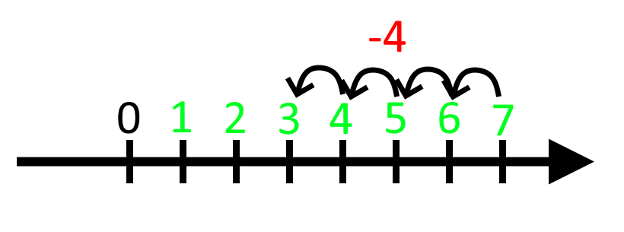
Når vi starter på et negativt tal, så fungerer det på ret meget samme måde. Vi kan starte på -3 og lægge 4 til:

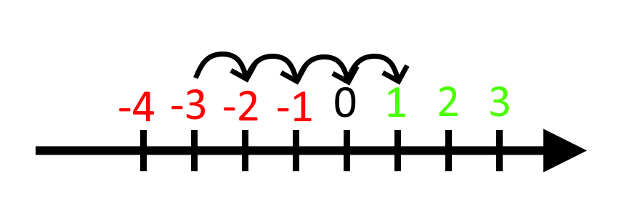
Og så lander vi på 1. Så derfor må -3 + 4 være 1.

Ud fra det vi har gennemgået, kan du så regne ud hvad -1 - 2 er? Prøv at se, om du kan regne den ud, inden du læser videre.

Når vi minusser, bevæger vi os mod venstre. Så hvis vi starter på -1 og trækker 2 fra, så går vi to skridt mod venstre:

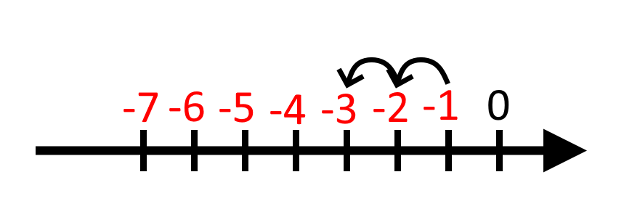
Altså er -1 - 2 = -3.

Det er lidt anderledes, når man lægger et negativt tal til, eller trækker et fra. Når man gør det, kan en huskeregel være, at man går i den modsatte retning af, hvad man ville gøre, hvis man skulle plusse eller minusse med et positivt tal.

Hvis vi starter på 2 og lægger -2 til, går vi to skridt mod venstre, som om vi trækker fra, selvom vi lægger til. Det ser sådan her ud:

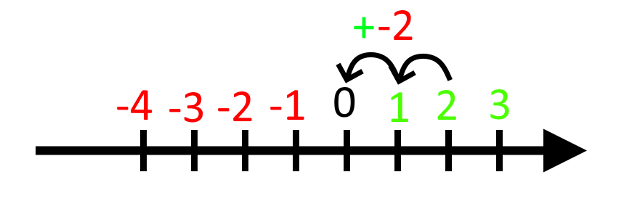
Altså er 2 + (-2) = 0.

Læg her mærke til, at når vi regner med negative tal, sætter vi nogle gange parenteser uden om det negative tal for at vise, hvor minustegnet hører til.

På samme måde kan vi trække negative tal fra. Når vi trækker et positivt tal fra, går vi mod venstre, så derfor går vi mod højre, når vi trækker et negativt tal fra:

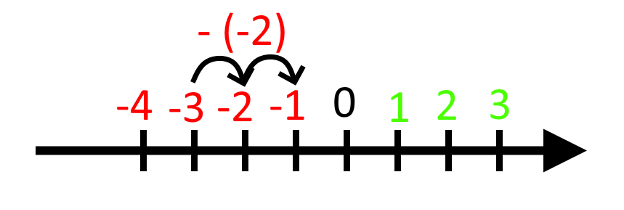
Når vi trækker (-2) fra -3 svarer det faktisk til, at vi plusser med 2. Derfor siger vi, at minus og minus giver plus.

Gange og division

Når man ganger med et negativt tal, bliver tallet vendt om til at være det modsatte af, hvad det var før. Så når man ganger:

• et positivt tal med et negativt tal, får man et negativt tal

• et negativt tal med et negativt tal, får man et positivt tal

På samme måde er det, når man dividerer:

• Hvis man dividerer et negativt tal med et positivt tal, får man et negativt tal.

• Hvis man dividerer et positivt tal med et negativt tal, får man et negativt tal.

• Hvis man dividerer et negativt tal med et negativt tal, får man et positivt tal.

Hvornår bruger vi negative tal?

Temperatur

Der, hvor vi finder flest negative tal udenfor matematiktimerne, er nok som temperaturer. Når det bliver vinter, og temperaturen falder til under frysepunktet, siger vi, at vi får minusgrader. Så har vi en temperatur, der er lavere end 0 grader.

Penge

Hvis man står i en situation, hvor man skylder flere penge væk, end man har, siger vi, at man har minus på kontoen, for så har man under 0 kroner.

Højde og dybde

Hvis man står på toppen af Mount Everest, står man 8.849 meter over havets overflade. Men hvis man i stedet dykker ned under havets overflade, begynder man at tale om negative højdemeter. Eksempelvis ligger skibet Titanic 3.800 meter under havets overflade, eller i -3.800 højdemeter.

Regneeksempler

Eksempel 1

Vi er givet regnestykket

$12+(-4)$

For at regne det ud, tegner vi det på en tallinje:

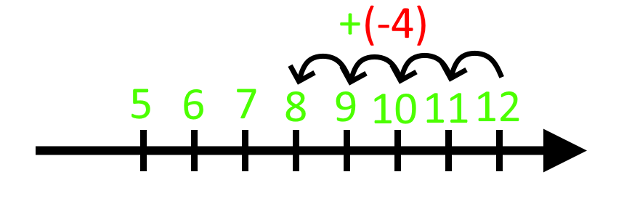
Altså er

$12+(-4)=8$

I stedet kan vi også regne ud, at når der kun står minus én gang, betyder det, at det svarer til, at vi minusser, og vi kan derfor skrive stykket op som 12 - 4, og det kender vi svaret på: 8.

Eksempel 2

Vi er givet regnestykket

$(-12)-3$

Mellem 12 og 3 står der kun minus én gang, og det må derfor svare til at minusse helt almindeligt. Vi går 3 skridt mod venstre på tallinjen, og det giver altså - 15.

Eksempel 3

Vi er givet regnestykket

$(-8)-(-8)$

Her er der mange minusser, så det kan være rigtig svært at regne ud. Vi starter fra venstre, og ser, at vi starter på (- 8). Derfra ser vi, at der et 2 minusser mellem tallene, og vi skal derfor gå mod højre, og vi skal gå 8 skridt. Det svarer altså til, at vi siger:

$(-8)+8$

Og det giver 0.

Eksempel 4

Vi er givet regnestykket

$(2-5)*3$

Her er det en fordel, hvis man er stærk til regnearternes hierarki. Vi starter med at regne det, der står inde i parentesen. Når vi har gjort det, har vi at:

$(-3)*3$

Når man ganger et positivt tal med et negativt tal, får man et negativt tal. Og 3 * 3 er 9. Altså må svaret være:

$(-3)*3=(-9)$

Ønsker du at blive klogere på negative tal, kan du se nedenstående video fra Restudy. På Restudy finder du mere end 2.000 undervisningsvideoer fordelt på 13 fag. Der er videoer om alt fra brøkregning, division, differentialregning og meget meget mere.