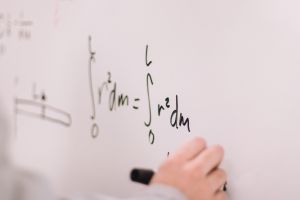Viden

Matematik

Toppunktsformlen

Artiklen er skrevet af

Sebastian Søndergaard
Mentor

20. september 2023

Toppunktsformlen: Udregning af toppunktet og alt imellem

Har du svært ved at huske på toppunktsformlen, eller blot leder efter smarte tricks til at tackle toppunktet bedre? Så har du fundet det rette sted, hvor jeg nu vil vise dig, hvordan toppunktsformlen anvendes. Hvorefter jeg til sidst vil vise, hvordan differentialregning også kan anvendes.

Fælles for alle andengradspolynomier er, at de har et toppunkt. Det er i dette punkt, hvor kurven har sit maksimum eller minimum. Kurven for et andengradspolynomium kaldes for en parabel. Hvis parablens grene er nedadgående, så er der tale om et maksimum. Modsat hvis grenene er nedadgående, så er det et minimum.

Figur udarbejdet på Geogebra

Toppunktsformlen

Formlen for at beregne et toppunkts koordinater er følgende:

$T_{p} (- \frac{b}{2 a}; - \frac{d}{4 a})$

Her svarer d til diskriminanten, som bl.a. bruges til at beregne rødderne for et andengradspolynomium, og er givet ved:

$d = b^{2} - 4ac$

a, b og c svarer til koefficienterne for det generelle andengradspolynomium

$f (x) = {ax}^{2} + bx + c$

Regne eksempel 1

Givet funktionen $f (x) = - x^{2} + 2x + 4$ beregn toppunktet til polynomiet:
Her ønskes at bestemme koordinaterne til toppunktet for funktionen:

f (x) = - x^{2} + 2x + 4

Her er koefficienterne:

a = - 1 : b = 2 : c = 4

x-værdien beregnes:

x = - \frac{2}{2 * (- 1)}

= \frac{- 2}{- 2}

= 1

y-værdien beregnes, herunder beregnes diskriminanten først:

d = 2^{2} - 4 * (- 1) * 4

= 4 + 16

= 20

d indsættes i udtrykket for y

y = - \frac{20}{4 * (- 1)}

= \frac{20}{4}

= 5

Toppunktet for funktionen f(x) er dermed $T_{p} (1; 5)$ . Hvilket er afbildet på figuren herunder:

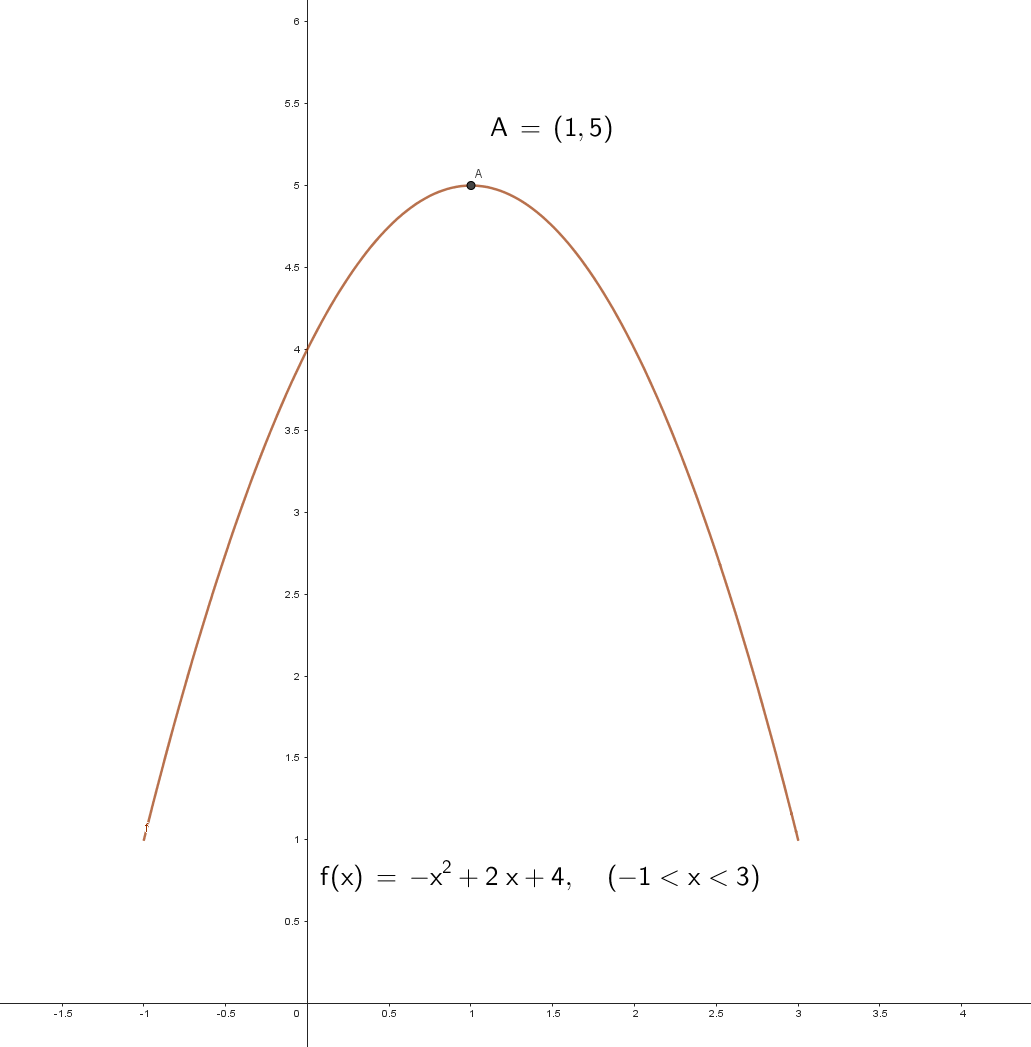
Figur udarbejdet på Geogebra.

Beregning af toppunktet vha. differentialregning

På matematik B bliver man præsenteret for differentialregning. Denne regneoperation gør det en del nemmere at beregne toppunktet til andengradspolynomiet, da differentialregning beskæftiger sig med tangenthældninger og hermed måden, hvorpå funktionen ændrer sig på, når man betragter en lille tilvækst i x- og y-værdierne. Se mere på differentialregning.

Toppunktet på et andengradspolynomium bliver også kaldt for et ekstremumspunkt, hvilket betyder, at det er her tangentens hældning ændrer fortegn, så den kan gå fra at være voksende til at være aftagende og omvendt.

Dette vil sige at for at findetoppunktet kan følgende ligning for funktionen løses for x:

f^{'} (x) = 0

Som kan læses som ”Til hvilken x-værdi opfyldes udtrykket, at tangentens hældning er lig 0” Hvilket sker i toppunktet.

Regne eksempel 2

Her ønskes at beregne toppunktet til samme funktion som i første eksempel. Her anvendes differentialregning i stedet for brug af toppunktsformlen.

f (x) = - x^{2} + 2x + 4

Funktionen f differentieres:

f^{'} (x) = - 2x + 2

Nu sættes den afledte funktion lig med nul og der løses for x:

f^{'} (x) = 0

- 2x + 2 = 0

Her lægges 2x til på begge sider.

- 2x + 2x + 2 = 2x

Leddene går ud med hinanden på venstresiden:

2 = 2x

Til sidst divideres der med 2

\frac{2}{2} = \frac{2x}{2}

x = 1

Førstekoordinaten til toppunktet er udregnet til at være 1.

x-værdien indsættes i funktion f

f (1) = - {(1)}^{2} + 2 * 1 + 4

f (1) = - 1 + 2 + 4

f (1) = 5

Toppunktet er hermed: $T_{p} (1; 5)$ .
Hvilket også giver det samme som i regneeksempel 1.

Placeringen baseret på fortegn

Toppunktets placering i koordinatsystemets fire kvadranter kan aflæses alene baseret på fortegnet af andengradspolynomiets koefficienter. Dette er smart at have i baghovedet, hvis man har lidt svært ved at skitsere et andengradspolynomium ud fra forskriften.

Igen betragtes andengradspolynomiet:

f (x) = {ax}^{2} + bx + c

Hvis a og b har samme fortegn: Toppunktet $T_{p}$ ligger i 2. eller 4. kvadrant

Hvis a og b har modsatte fortegn:

Toppunktet $T_{p}$ ligger i 1. eller 3. kvadrant