Differentialregning

Intro

Matematik i 2.g starter for de fleste med at blive introduceret til emnet differentialregning, men hvad er differentialregning? Det vil jeg i løbet af det næste stykke tid præsentere for dig. Som alt andet i matematik, er det altid en god idé at kigge på nogle eksempler.

Du skal nu forestille dig, at du tager en løbetur på 100 meter. Din ven står ved siden af, tager tid, og tjekker hvor langt du er efter 1 sekund, 2 sekunder osv. Indtil du er oppe på de 100 meter. Så kan I spørge hinanden, hvor hurtigt løb du i gennemsnit? hvilket er en nem beregning, nemlig $\frac{\Delta t}{100m}$ , hvor $\Delta t$ er den tid du brugte på løbeturen. Du har højst sandsynligt ikke løbet lige hurtigt i alle 100 meter. Måske løb du allerhurtigst til sidst, og ikke særligt hurtigt lige i starten. For at beregne en øjeblikshastighed, kommer differentialregning ind i billedet.

Hældningskoefficient

For at kunne bestemme en hældning i et helt præcist punkt, skal vi opstille en funktion, der kan fortælle os noget om verdenen vha. matematiske modeller. Her ser på funktionen $f\left(x\right)=x^2$. Funktionen $x^2$ danner den her næsten U-formet figur, som har minimum (toppunkt) i punktet (0,0).

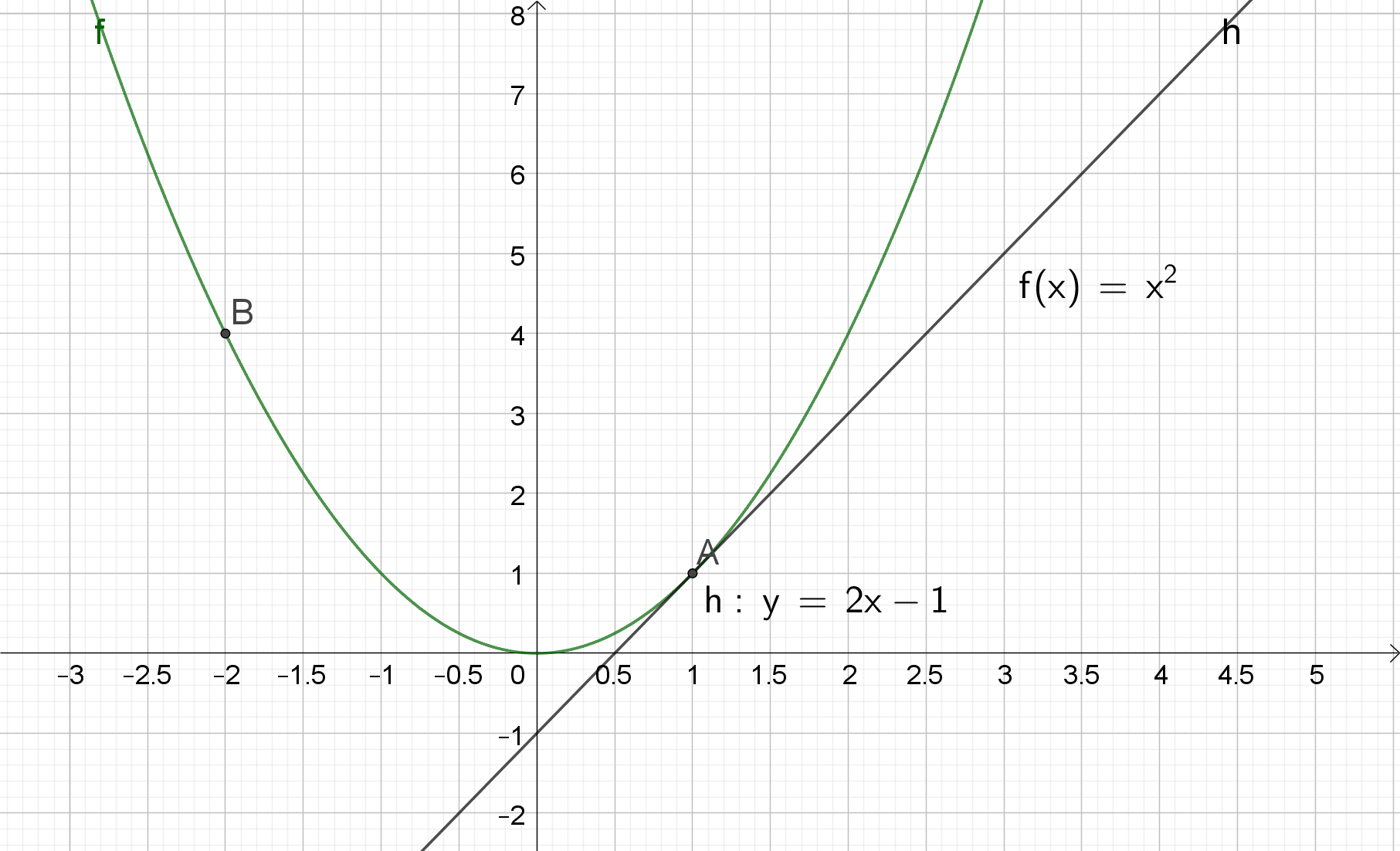
Lad os se på punktet A, med koordinatsættet (1,1). For at finde hældningen i punktet, hvilket også kaldes hældningskoefficienten, kunne man gætte sig frem, ved at tegne streger der går lige gennem punktet, og så efterfølgende aflæse hældningen vha. formlen $a=\frac{y_2-y_1}{x_2-x_1}$.

I matematik er vi dog ikke særligt glade for at gætte os frem til resultater, derfor benytter vi os af differentialregning. Vi ønsker nu at finde den afledede funktion, hvilket betyder, at vi differentierer funktionen ƒ. Til at hjælpe os med dette, kan man åbne sin formelsamling - jeg har vedhæftet et link til den officielle formelsamling, som jeg fremover vil henvise til. Slå op på side 24 og find formel (133).
Her ser vi, at hvis funktionen hedder noget med $x^a$, altså en potensfunktion, så er den afledede funktion $\mathit{a·}{x}^{a-1}$. Vi ser nu, at vores funktion $x^2$, ligner $x^a$, vi erstatter derfor a’et med et 2-tal:

Vi kan derfor bestemme, at den afledede funktion for $x^2$ må være $2x$. Det kan skrives på flere forskellige måder, hvor alle er lige rigtige, har herunder skrevet 3 forskellige måder, der alle er lig med $2x$:

Endelig kan vi beregne hældningskoefficienten for punktet A(1,1). Det er simpelt, vi indsætter bare x-værdien fra punktet ind i vores afledede funktion, se herunder:

Vi kan derfor konkludere, at hældningskoefficienten i punktet A(1,1) er lig 2.

Tangenter og sekanter

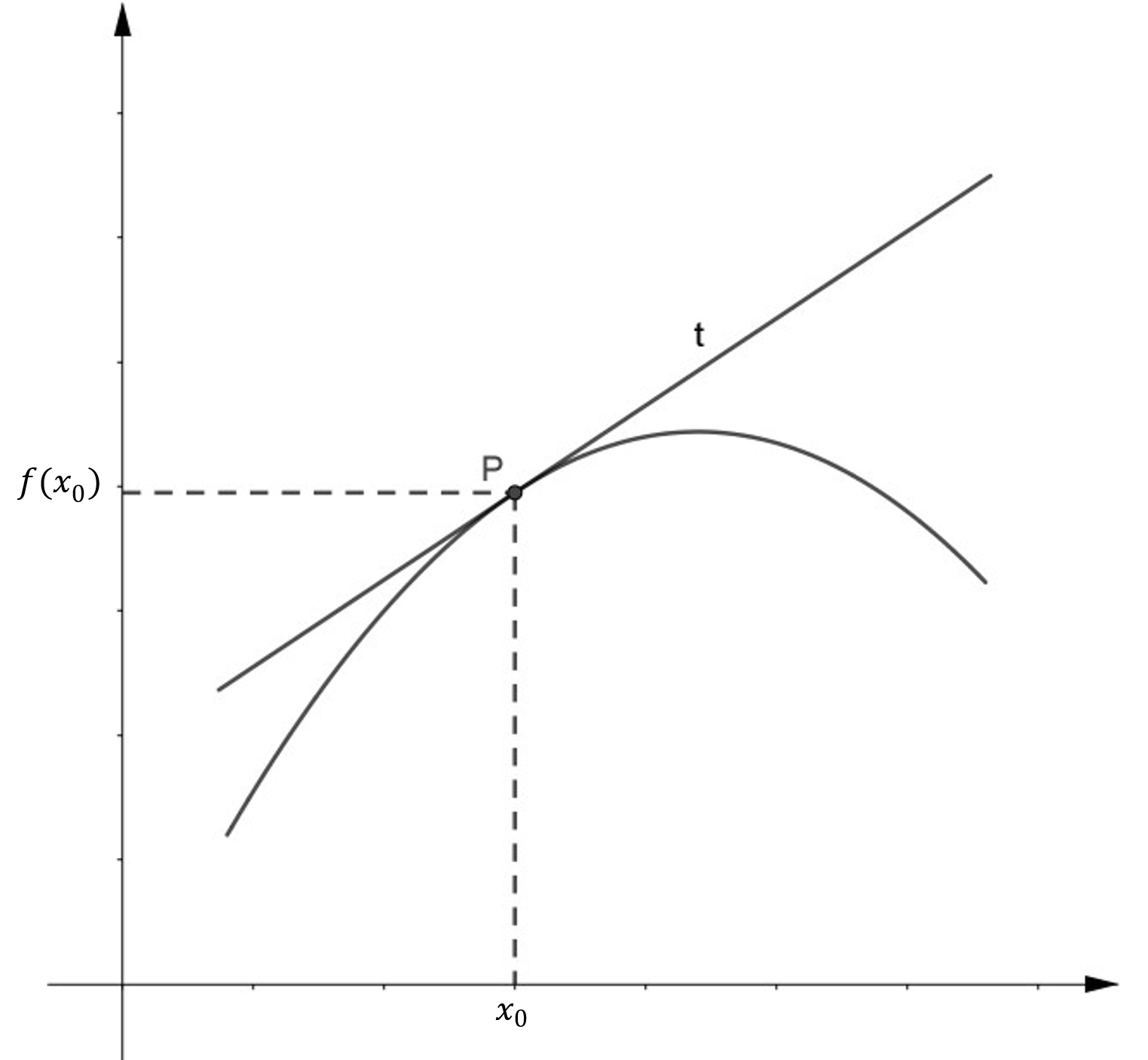
I differentialregning, vil vi gerne finde hældningen i et punkt, for at kunne opstille en tangent. En tangent er en ret linje, med formlen $f\left(x\right)=\mathit{ax}+b$, der går gennem et punkt, som f.eks. kunne hedde $\left(x_0,f\left(x_0\right)\right)$. For at kunne finde vores tangent, bliver vi nødt til at bruge en sekant. Sekanten er en ret linje, der går gennem 2 punkter på funktionen, se figur nedenfor:

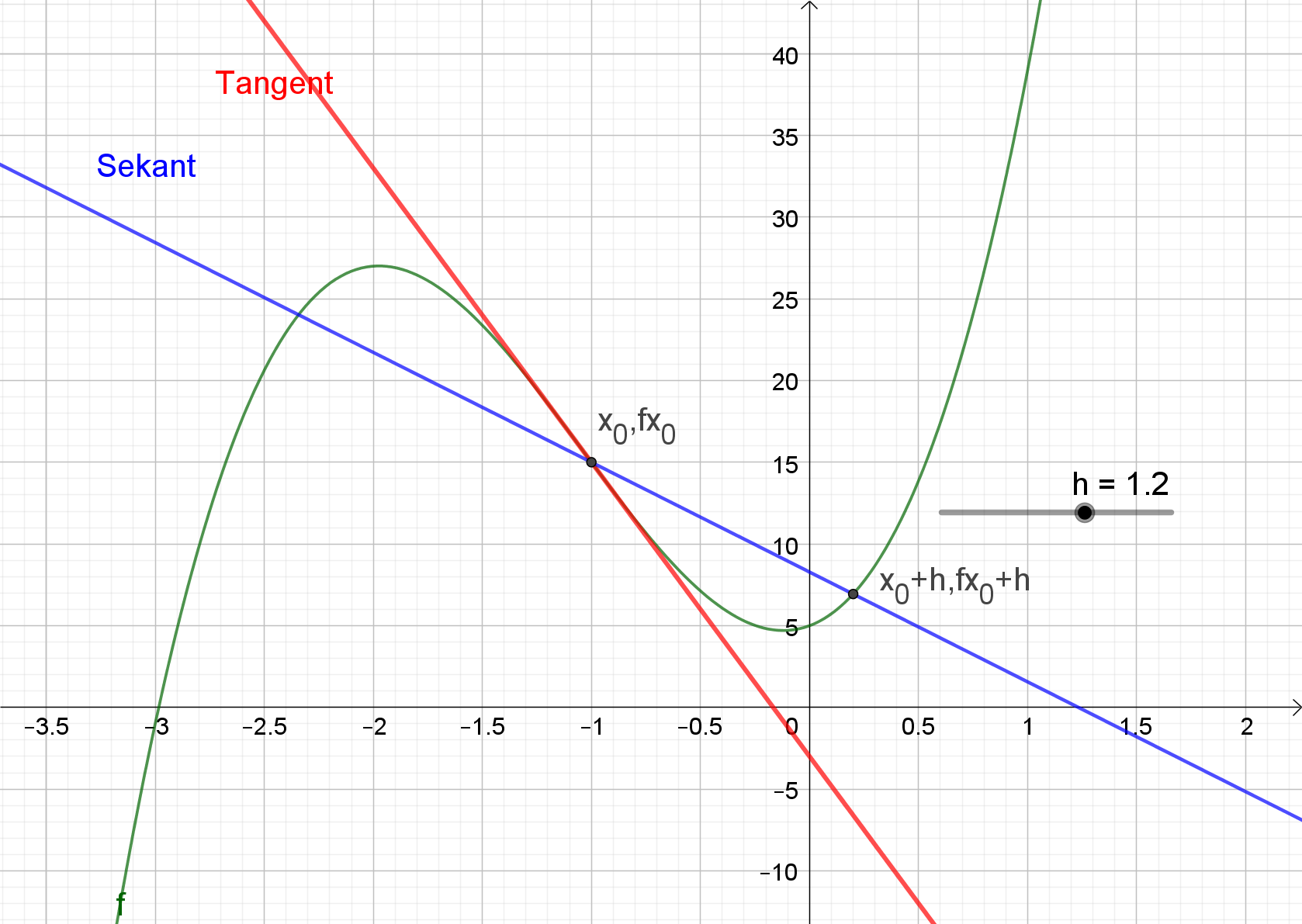
Vi opstiller vores sekant, ved at tage vores første punkt på funktionen, som vi kaldte $\left(x_0,f\left(x_0\right)\right)$, og derefter lægge et $h$ til. Her skal du forestille dig, at $h$’et er et lille stykke du går ud på x og y-aksen, så punktet ikke ligger helt oven i det første punkt. Vi siger derfor, at sekanten går gennem punkterne $\left(x_0,f\left(x_0\right)\right)$ og $\left(x_0+h,f\left(x_0+h\right)\right)$. For at beregne en hældningen for en ret linje, hvilket sekanten er, åbner vi nu igen formelsamlingen, og finder formel (63), som lyder: $a_{\mathit{sekant}}=\frac{y_2-y_1}{x_2-x_1}$. Ved at indsætte vores 2 punkter fra sekanten, kan vi finde hældningen for sekanten:

Vi har nu en hældning for vores sekant, hvilket vi skal bruge til næste emne, nemlig 3-trinsreglen.

3-trinsreglen

Vi benytter 3-trinsreglen til at bestemme vores tangenthældning, også kaldet differentialkvotienten, i punktet $x_0$. Vi vil herunder tage udgangspunkt i samme funktion som før, nemlig $f\left(x\right)=x^2$.

Første trin lyder på, at vi opskriver vores differenskvotient. Bemærk at der er forskel på differenskvotient og differentialkvotient. Vi bruger differenskvotienten fra forrige afsnit, hvor vi havde fået hjælp fra formel (63).

Vi indsætter nu vores funktion $x^2$

I andet trin skal vi reducere vores udtryk. Her bruger man ofte matematiske regneregler, eller tilføjer/fjerner led/udtryk til differenskvotienten. I vores eksempel bruger vi kvadratsætningen ${\left(a+b\right)}^2=a^2+b^2+2\mathit{ab}$

Opdeler brøk med fællesnævner:

Vi har nu reduceret vores differenskvotient til $h+2x_0$. Husk det også er vores sekanthældning.

Til sidst ønsker vi at undersøge den såkaldte grænseværdi for $h\to 0$, hvilket skal læses som ”h går mod 0”.

Vi skal nu forestille os, at $h$’et bliver mindre og mindre, jo tættere det kommer på 0. På den måde, bevæger sekanten sig tættere på tangenten, da de 2 punkter kommer uendeligt tæt på hinanden, dog uden nogensinde at ramme hinanden helt, da man så ikke ville kunne beregne en hældning. Vi siger derfor, at $h$ bevæger sig så tæt på 0 som muligt. I praksis skriver vi at $h=0$, men hvis censor spørger, så er $h$ ikke 0.

Hvis $h\to 0$ så (næsten) $0+2x_0=2x_0$

Vi kan nu konkludere, at vores differentialkvotient er $2x_0$, ergo:

Ligning for tangenten

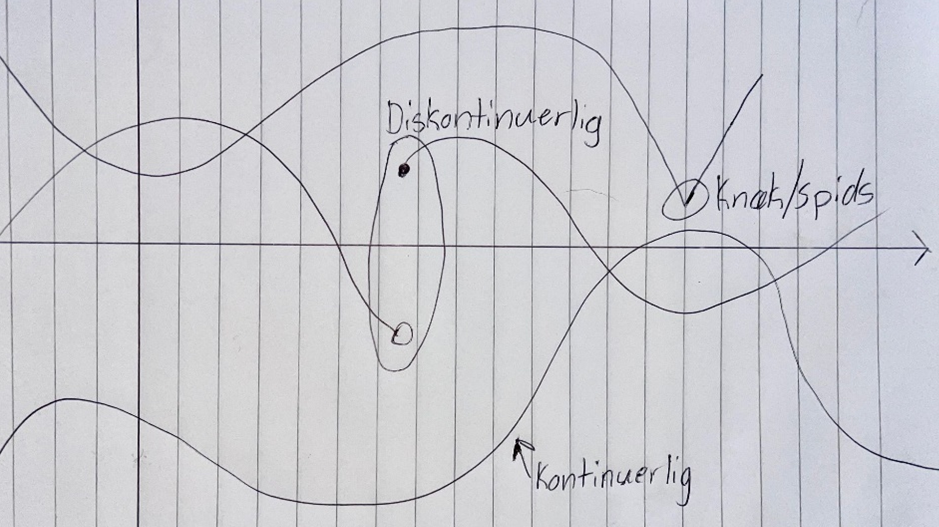
Ovenfor har vi lige undersøgt, hvordan vi finder hældningen for en tangent. Nu vil vi prøve at finde ligningen for en tangent. Før man overhovedet må differentiere en funktion, skal man sikre sig, at den er differentiabel. Det vil sige, at den skal være kontinuerlig og uden knæk. Den må altså ikke springe rundt på koordinatsystemet, og den må ikke være spids ved dens toppunkter. Når man har sikret sig, at den er differentiabel, så kan man finde en ligning for tangenten.

Vi bruger samme formel som før, nemlig formel (63), $a=\frac{y_2-y_1}{x_2-x_1}$. Denne formel finder hældningen for en ret linje vha. 2 punkter. Vi vælger nu at modificere formlen lidt, så den i stedet hedder:

Vi ønsker nu at isolere for y. Vi starter med at gange med $(x-x_0)$ på begge sider:

Fra 3-trinsreglen ved vi, at $a=f\text{'}(x)$, og fra formelsamlingen ved vi, at $y_0=f(x_0)$, derfor erstattes det i formlen:

Ved at skifte om på ledende, så får vi formel (121) i formelsamlingen:

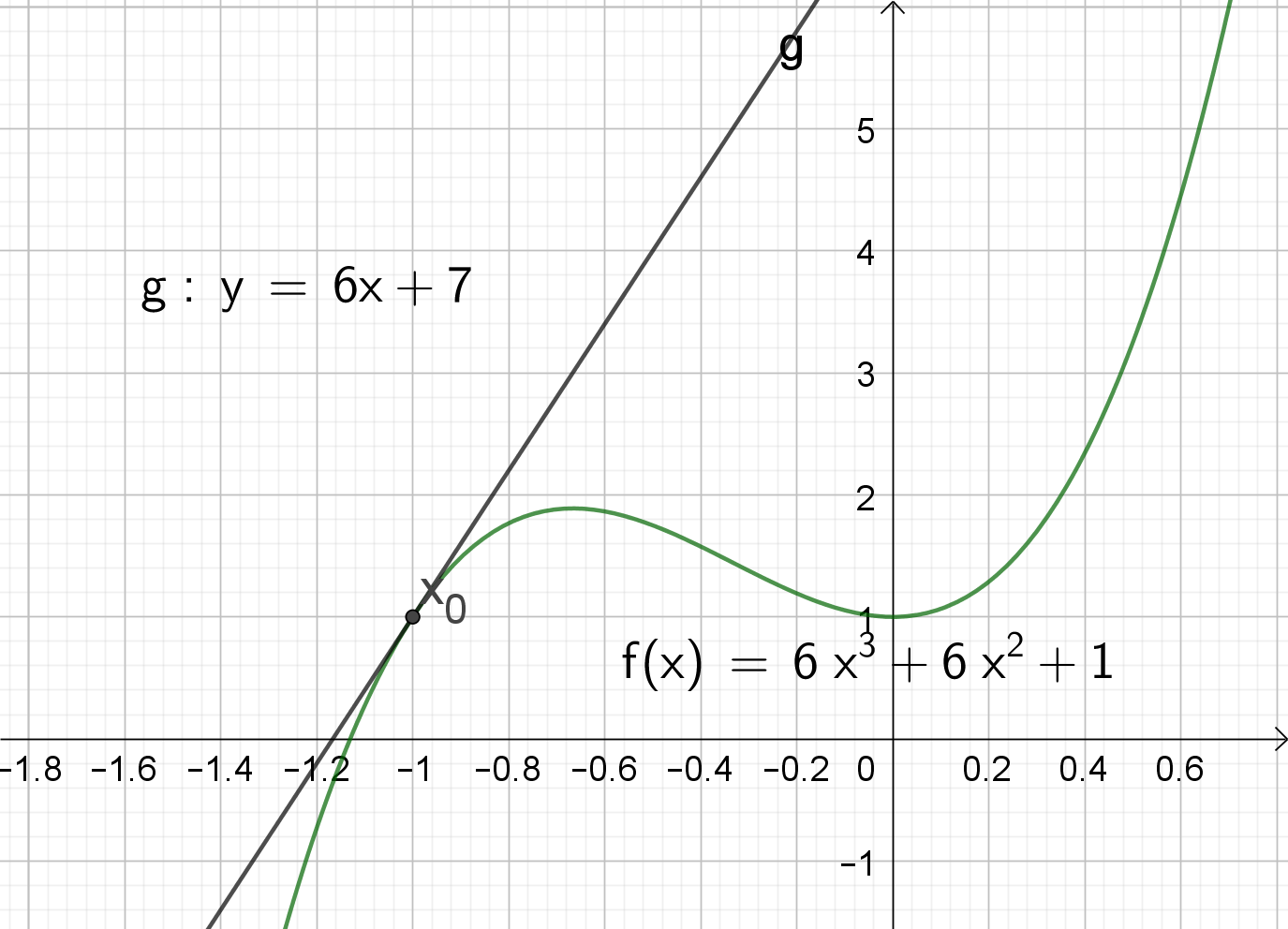
Vi prøver nu at lave et regneeksempel, med nedenstående funktion:

Og vi vil finde tangenten i punktet $\left(-1,f\left(-1\right)\right)$, ergo $x_0=-1$

Vi starter med at finde vores ligning for tangenten:

For at finde $f(x_0)$, sætter vi bare $-1$, altså vores $x_0$-værdi ind i funktionen:

Det betyder altså, at vores $f(x_0)$-værdi er 1.

For at finde $f\text{'}(x_0)$, starter vi med at differentiere vores funktion. Her benytter vi formel (133) og (128)

Nu indsætter vi vores $x_0$-værdi:

Vi indsætter nu vores $f\text{'}(x_0)$ og $f(x_0)$ værdier i ligningen:

Nu ganger vi ind i parentesen:

Ergo lyder ligningen for tangenten, til punktet $\left(-1,f\left(-1\right)\right)$ til:

$y=6x+7$

Formelsamling:
https://emu.dk/sites/default/files/2019-02/Formelsamling-Matematik-B---stx-2018.pdf