Cirklens dele
Når vi i matematik taler om cirkler, har vi nogle begreber, som vi tit bruger. De begreber gennemgår vi fra en ende af. Den første, vi vil tage et kig på, er cirkelbuen. Cirkelbuen er den streg, der udgør selve cirklen:

Længden på cirkelbuen er det mål, som vi kalder omkreds (O). Længere nede i artiklen ser vi på, hvordan vi udregner omkredsen af en cirkel.
Præcis i midten af cirklen har vi et punkt, som vi kalder centrum (C):
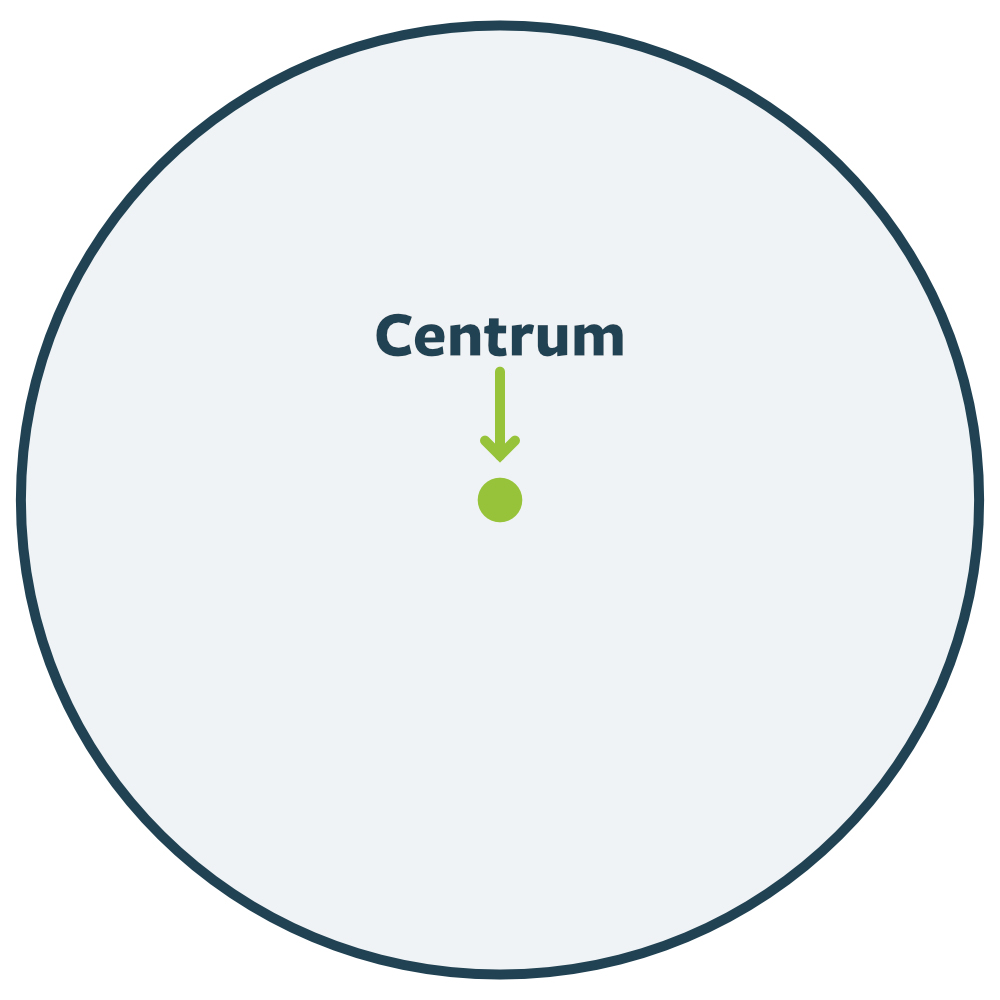
Mellem centrum og cirkelbuen kan vi tegne en streg. Den kalder vi radius (r):
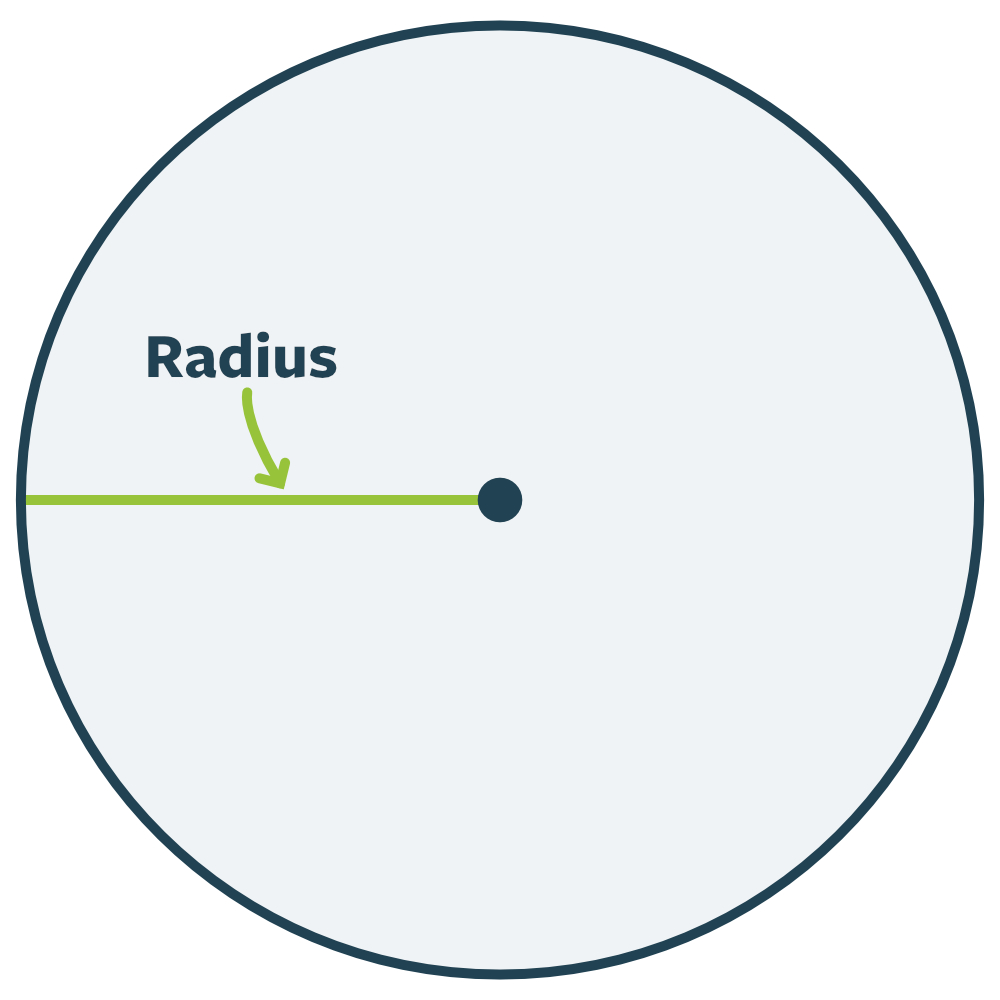
Det er vigtigt at påpege, at alle streger mellem centrum og cirkelbuen er radius. Så selvom vi har tegnet den på en måde, er der altså mange forskellige “radiusser” i en cirkel - og de har alle samme længde.
Det næste, vi skal have styr på, er den streg, der går fra cirkelbue til cirkelbue igennem radius. Den kalder vi diameteren (D):
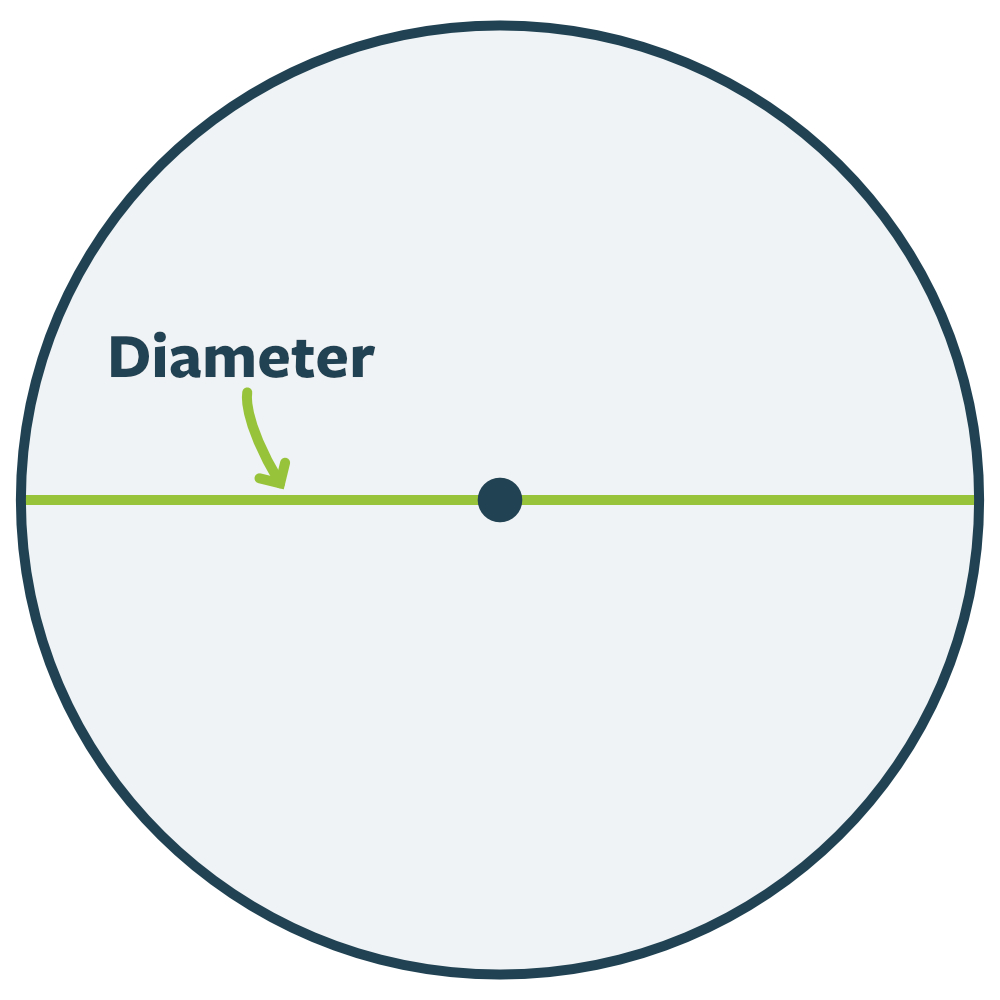
Man kan også vælge at se på diameteren som den dobbelte radius, da den består af netop to streger, der går mellem cirkelbue og centrum.
Det sidste begreb vi skal have med os, inden vi begynder at regne på cirklen, er cirklens areal (A). Det er alt det inde i cirklen:
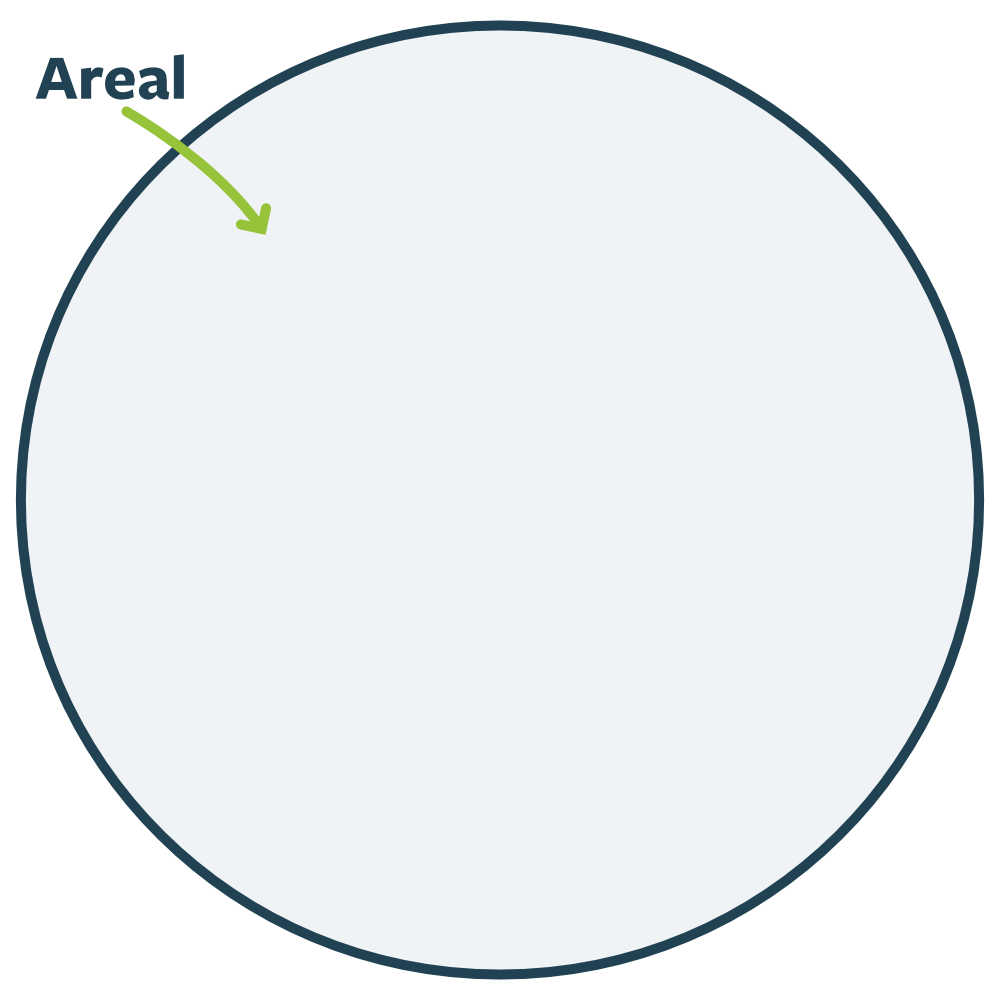
Areal og omkreds er begge rigtig svære at måle, så derfor beregner vi dem ret ofte. Det kigger vi på i næste afsnit.
At beregne areal og omkreds
Når vi beregner areal og omkreds, er vi nødt til at kende til et helt bestemt tal: π (pi).
π er et tal, der beskriver forholdet mellem en cirkels diameter og dens omkreds. Hvis vi skal skrive π som et decimaltal, så skriver vi oftest 3,14, men i virkeligheden er π uendelig langt med for altid skiftende decimaler. De første 10 cifre i pi er 3,141592653 (find den første million cifre her). Men når vi regner med π, bruger vi oftest bare 3,14.
Fordi π er forholdet mellem en cirkels diameter og dens omkreds, er vi så heldige, at vi bare skal gange diameteren med π for at få omkredsen.
Altså er formlen for omkreds:
Når vi skal beregne areal, skal vi igen bruge π, denne gang sammen med radius. Formlen for arealet af en cirkel er:
Vi kigger videre på både areal og omkreds i afsnittet “regneeksempler” længere nede på siden.
Tangenter og korder
Tangenter og korder er også begreber, der er rigtig fine at have godt styr på, når vi taler om cirkler. En tangent er en ret linje, der rører ved cirkelbuen i kun ét punkt.
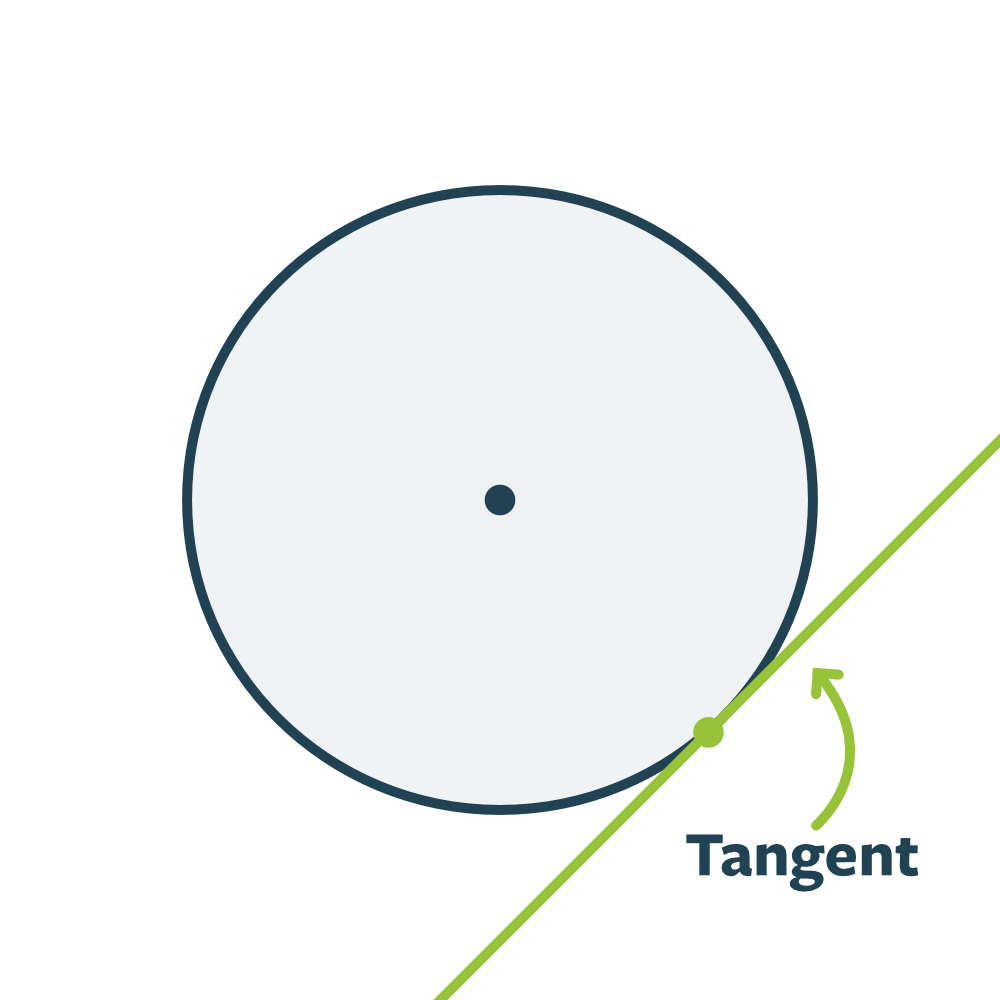
En korde er en ret linje, der rører ved to punkter på cirkelbuen:
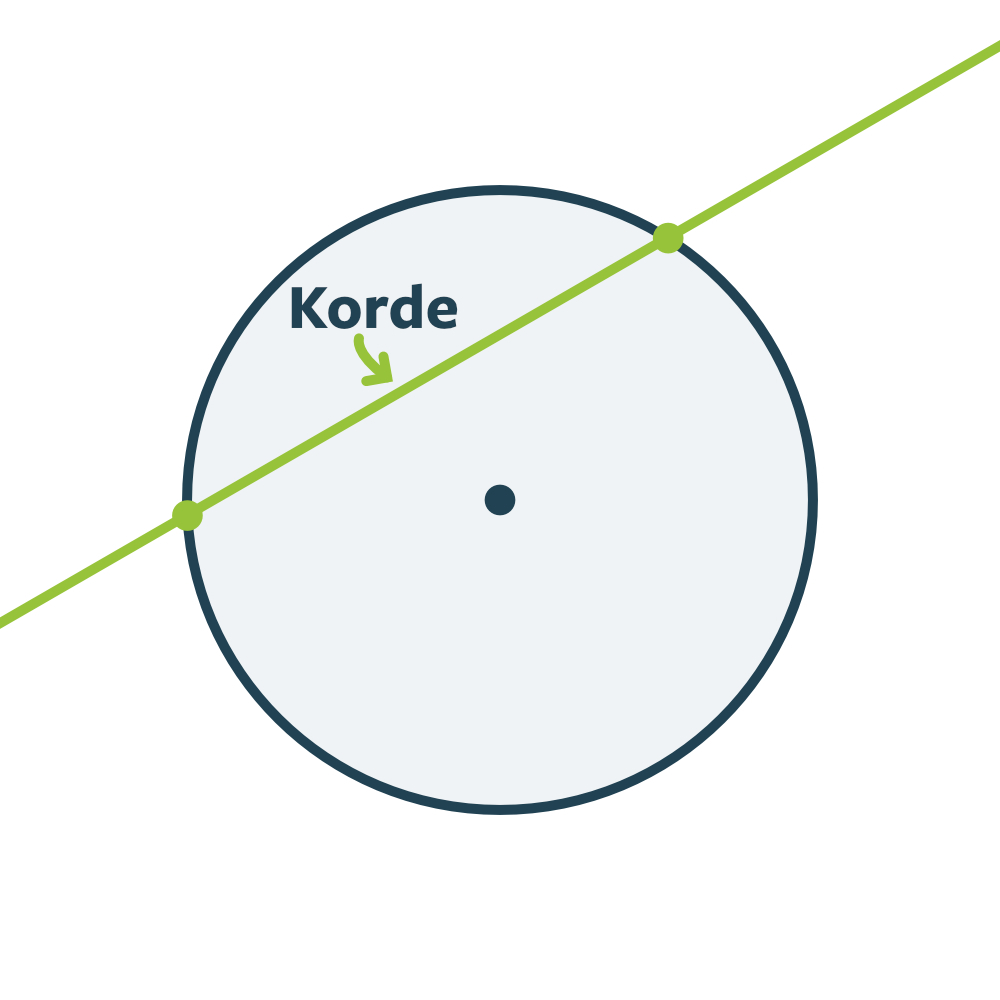
Tidligere så vi på den korde vi bruger mest: diameteren.
Regneeksempler på cirkler
Eksempel 1
Vi er givet en cirkel med en radius på 10 cm. Vi får at vide, at vi skal beregne arealet. Overvej et øjeblik, hvordan du vil gribe sådan en opgave an, inden du læser videre.
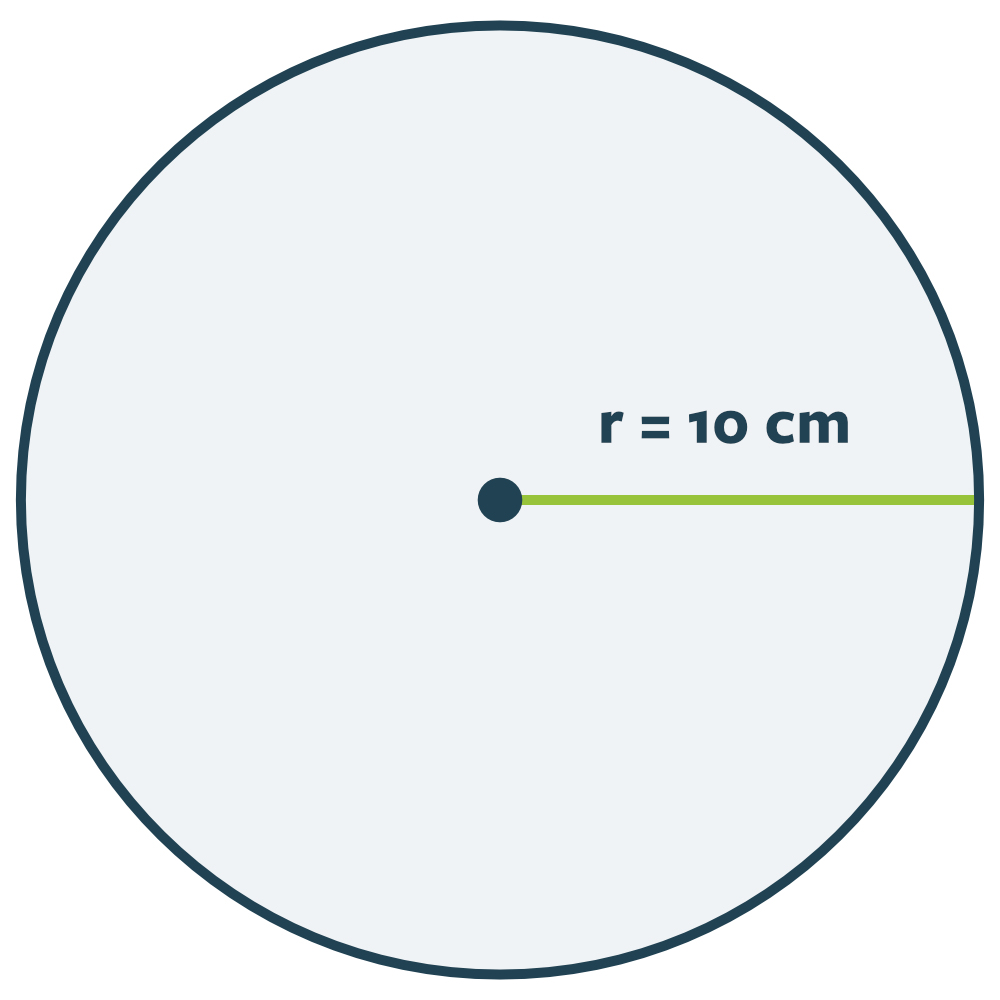
For at finde arealet, sætter vi vores radius ind i formlen for areal:
Når vi skal gange med π, kan det nogle gange være en fordel at lave et overslag, ved bare at gange med 3:
Hvis vi gerne vil have et svar, der er tættere på det rigtige, kan vi gange med 3,14:
Hvis vi gerne vil endnu tættere på, kan vi bruge vores lommeregner, hvis den har en π-knap:
Altså er cirklens areal 314,159… kvadratcentimeter.
Eksempel 2
Vi er givet en cirkel og fået at vide, at dens omkreds er 19 cm. Vi bliver bedt om at finde frem til radius. Tænk et øjeblik over, hvordan du vil tackle en sådan opgave, før du fortsætter med at læse.
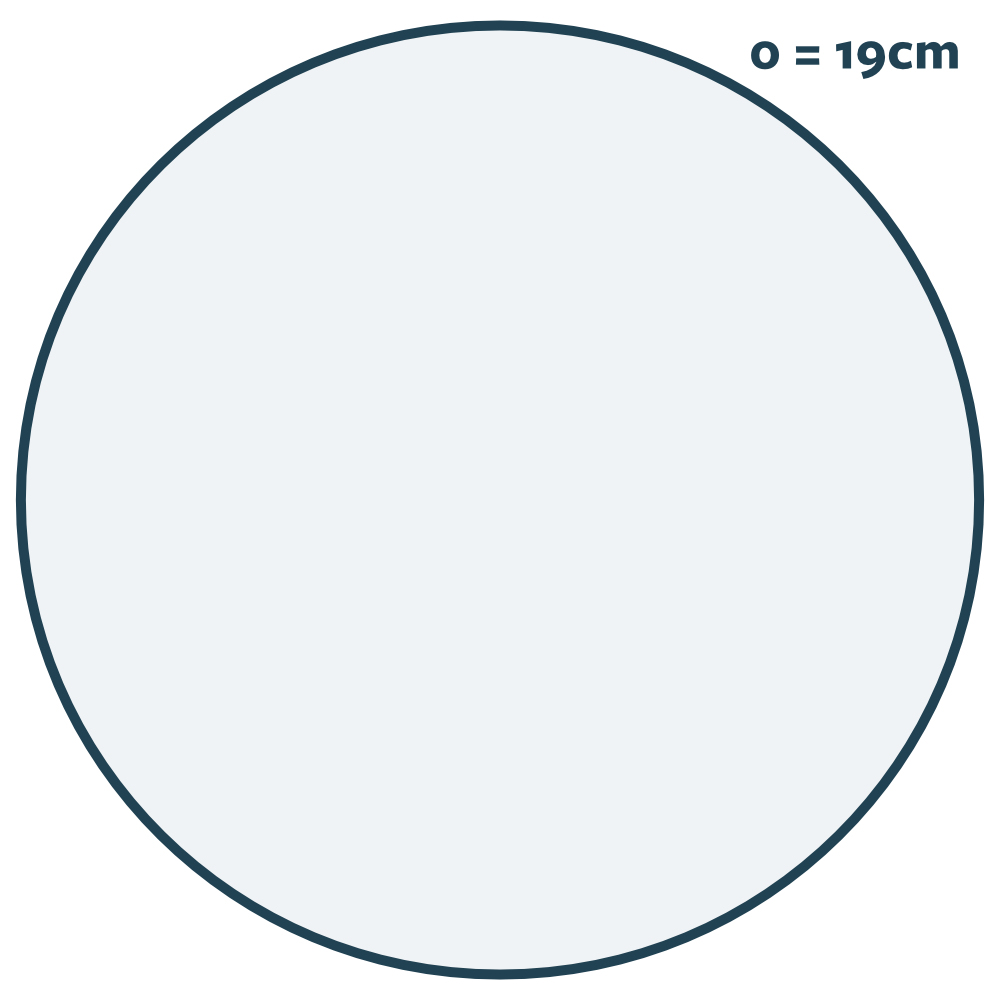
For at kunne beregne radius ud fra omkredsen, er vi nødt til at kende en formel, hvor begge værdier indgår. Sådan en kan vi lave. Vi tager udgangspunkt i formlen for omkreds:
Vi ved, at diameteren også kan skrives som den dobbelte radius. Det kan vi skrive ind i formlen:
I den her nye formel indgår både omkreds og radius. Så med den kan vi beregne radius ud fra omkreds. Vi starter med at sætte vores værdi for omkreds ind:
Nu har vi opstillet en ligning, den kan vi løse ved at dividere med 2 og π på begge sider af lighedstegnet:
Altså er cirklens radius 3.
Hvad ved vi om cirkler?
Nu har vi gennemgået cirklens hovedtræk, såsom dens radius, diameter, areal og omkreds. Vi har kigget på, hvordan man beregner hovedtrækkene, og hvilke egenskaber de forskellige har. Vi har også kigget kort på og talt om, hvad dens betydning for cirklen egentlig er.
God fornøjelse med cirklerne i matematik!