I denne artikel vil vi kigge kort på, hvordan man finder volumen eller rumfanget af en cylinder. Bagefter vil vi kort gennemgå, hvordan man finder overfladearealet af en cylinder og så se på, hvad forskellene på de to mål er.
Rumfanget af en cylinder
Når vi taler om rumfang, så taler vi om et tredimensionelt mål, og om hvor meget noget fylder. Eksempelvis er rumfanget af en sodavandsdåse cirka 33 cl, altså den mængde væske, der kan være indeni. Til at beregne rumfanget af en cylinder, bruger vi en formel, der hedder , hvor r er cylinderens radius, h er cylinderens højde, og V er rumfanget. Vi tager udgangspunkt i netop en sodavandsdåse, som vi målet højde og radius på:
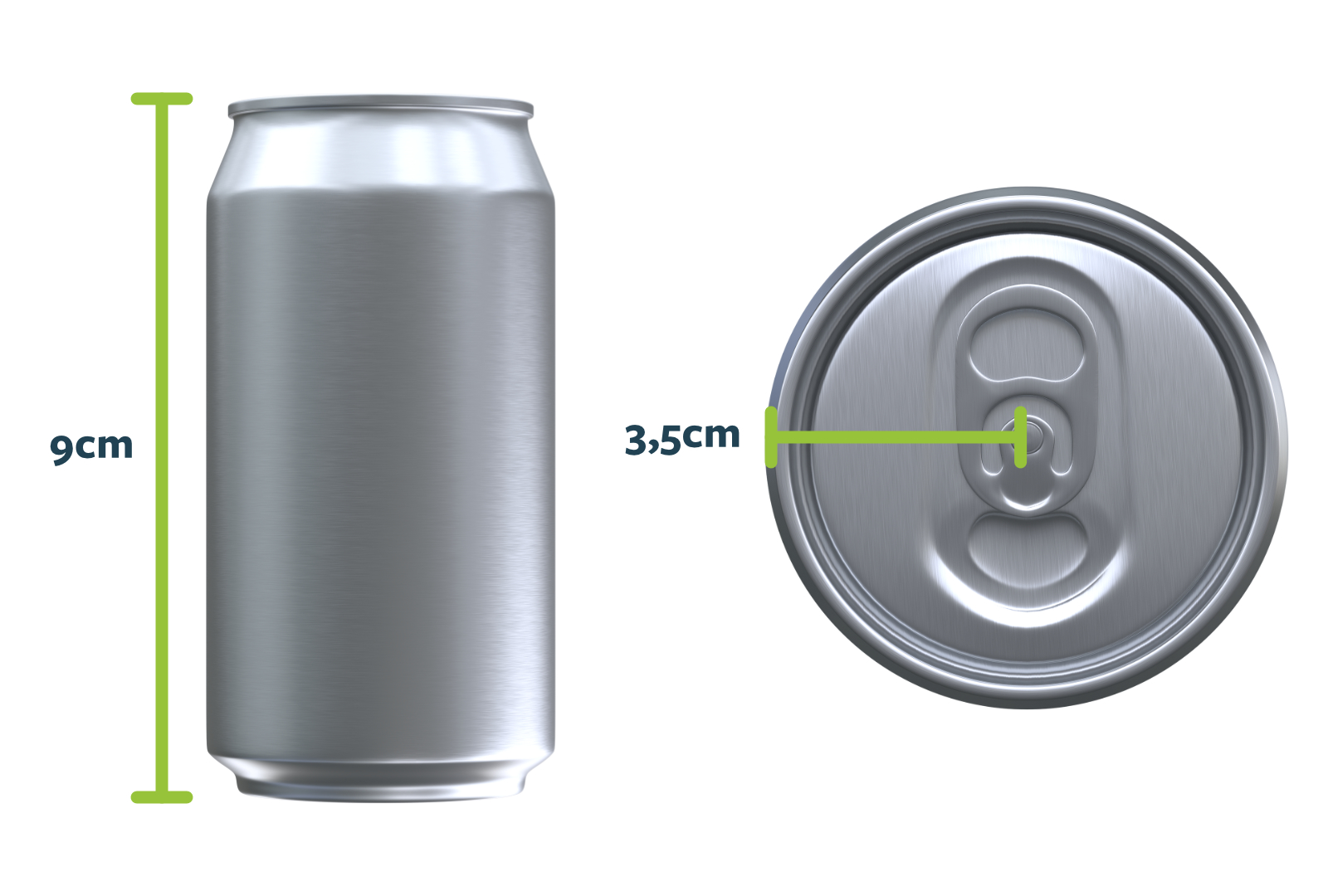
Målene af dåsen lægger vi ind i vores formel:
Der skal 10 cm3 til 1 cl, så dåsens rumfang er knap 35 cl. Hvis vi så tager i betragtning, at den nok ikke er fyldt til randen med sodavand, og at den ikke er en perfekt cylinder, så passer det nok meget godt, at der er 33 cl sodavand i dåsen.
Formlen for rumfang
Når vi finder arealet af en cylinder, finder vi faktisk først arealet af den cirkel, der udgør toppen og bunden af cylinderen. Formlen for en cirkels areal er A = r2 * π. Du kan læse mere om cirkler i vores artikel "Radius, areal og omkreds: en guide til cirkler i matematik".
På den ganger vi cylinderens højde, fordi cylinderen helt grundlæggende er en masse cirkler, der ligger ovenpå hinanden.
Overfladearealet af en cylinder
Når vi taler om overfladearealet, så taler vi om, hvor stor en overflade et tredimensionelt objekt har. Det er det areal, sodavandsdåsen ville have, hvis vi skar den ud og lagde den fladt ned.
Formlen for overfladearealet af en cylinder lyder: , hvor r er radius, h er højde, og er overfladearealet. Hvis vi tager udgangspunkt i målene for sodavandsdåsen, vi havde før, ser beregningen af overfladearealet sådan ud:
Aluminiumet, som dåsen er lavet af, har altså et samlet areal på
Formlen for overfladeareal
Når man kigger nærmere på formlen for overfladearealet af en cylinder, kan man se, at den er delt op i to dele, som er adskilt af et plustegn.
Den første del lyder:
. Denne del beregner arealet af cylinderens top og bund, som er to cirkler. Det er altså 2 gange arealet af en cirkel,
.
Den anden halvdel af formlen for overfladeareal,
handler om arealet af den krumme overflade (altså den bøjede del). Hvis man folder den ud, får man et rektangel, hvis ene side har cylinderens højde som længde, og hvis anden side har den cirkel, der udgør toppen og bundens omkreds, som længde. Man udregner omkreds af en cirkel ved at sige
Altså er den krumme overflades areal
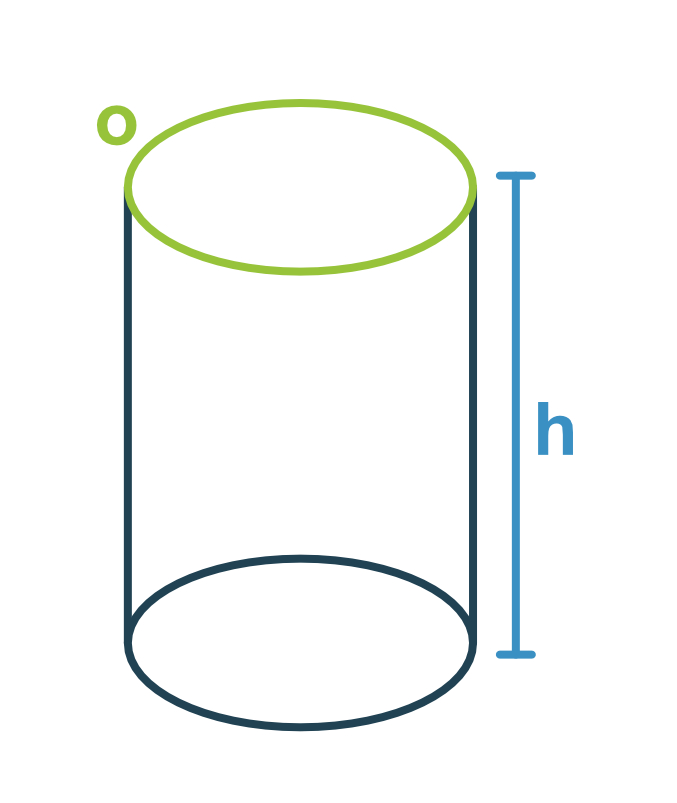
Det kan godt være lidt svært at visualisere, så her er det demonstreret med en toiletrulle. Her er topcirklens omkreds og højden på toiletrullen tegnet ind:
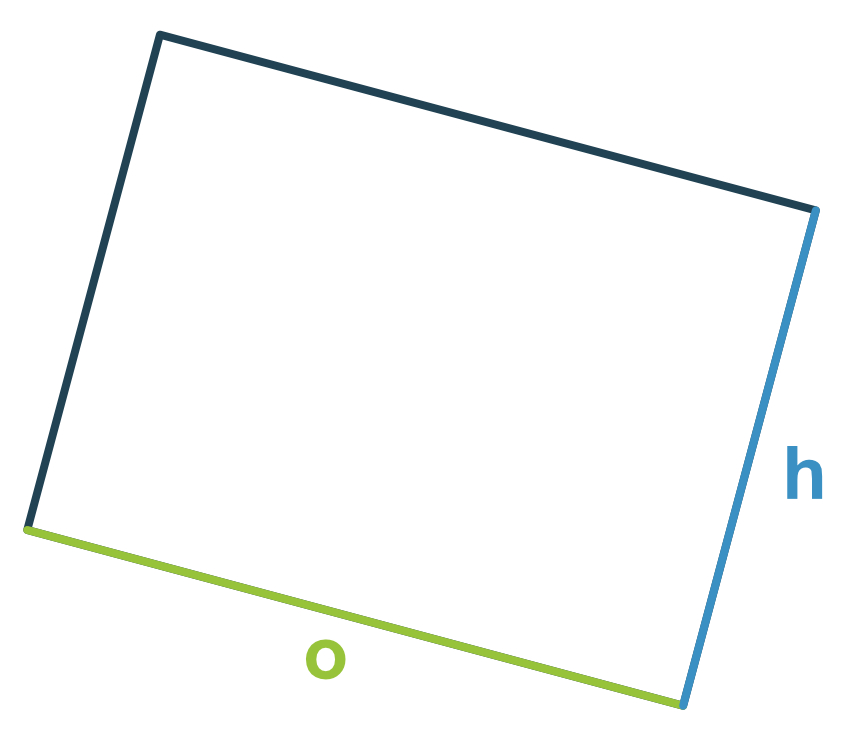
Her er toiletrullen klippet op, men højde og omkreds er stadig markeret. Som vi kan se, er toiletrullen et rektangel, så vi må gange siderne med hinanden for at få arealet!
Rumfang og overfladeareal
Nu har vi undersøgt, hvordan man finder både rumfang og overfladeareal af en cylinder. Vi har fået forståelse for, at rumfanget af en cylinder betyder noget for, hvor meget den fylder, og at overfladearealet beskriver, hvor meget materiale der skal til for at lave en cylinder. Vi har kigget på, hvordan de to formler er opbygget, og hvilke mål man skal bruge for at udregne både rumfang og overfladeareal.
Video om rumfang, og hvordan man finder det
I denne video fra Restudy kan du lære mere om rumfang, og hvordan man finder det. I videoen gennemgår vi rumfang af cylinder, pyramide, kegle og prisme.
Du kan se mange flere videoer om matematik og få hjælp til faget på Restudy.