Det grundlæggende om brøker
En brøk er en måde, man i matematikken repræsenterer en del af noget. Det kan eksempelvis være et stykke af en pizza. Hvis man har en pizza som den nedenfor og skærer den ud i 4 lige store stykker, vil hvert stykke være
af den oprindelige pizza.
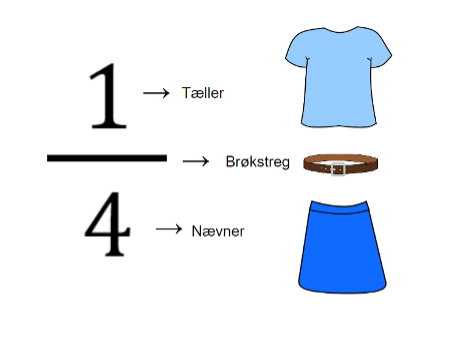
Brøker er sammensat af tre dele: Hvis man vil have en huskeregel for at huske det, kan man tænke på, at Tælleren eller T-shirten er over Nævneren eller Nederdelen, og at de er adskilt af Brøkstregen eller Bæltet.
For at forstå brøkers betydning, er det vigtigt, at vi forstår brøkers størrelser. Generelt kan man sige, at hvis der er meget stor forskel på tæller og nævner som i f.eks. brøken
er den lille, hvorimod en brøk som
hvor forskellen er lille, er meget tættere på at være en hel.
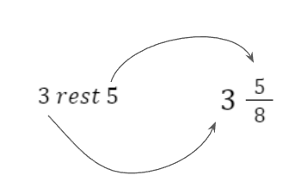
Hvis tælleren er større end nævneren, er der tale om en såkaldt uægte brøk. Dette betyder, at brøken er større end én hel. Man kan omskrive uægte brøker til et heltal og en brøk. Det kan man gøre ved at dividere tælleren med nævneren og finde resten. Hvor mange hele gange nævneren går op i tælleren er heltallet, og resten er den nye nævner. Det kan se sådan her ud: Vi er givet en uægte brøk, hvor tælleren er større end nævneren. . Og omskriver det til en ægte brøk og et heltal:
Omskrevet til en ægte brøk og et heltal er
På samme måde man kan regne med heltal, kan man også regne med brøker:
Hvis vi vil lægge brøker sammen eller trække dem fra hinanden, er de nødt til at have den samme nævner, det vi kalder en “fællesnævner”. Fællesnævner finder man ved at forlænge eller forkorte brøkerne.
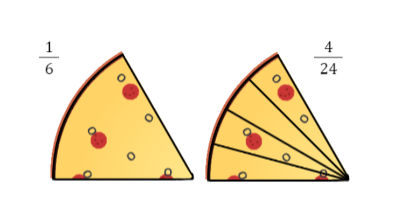
Når vi ganger med samme tal i både tæller og nævner, sikrer vi, at selvom tallene ændrer sig, bliver brøken hverken større eller mindre.
Når man har fundet fællesnævner mellem brøkerne, kan man begynde at plusse og minusse med dem: For at lægge to brøker med fællesnævner sammen, lægger man blot tællerne sammen og beholder nævneren. Lad os regne videre med tallene fra før:
Altså er
Når man trækker brøker fra hinanden, foregår det på ret meget samme måde, som når man lægger dem sammen. De skal have en fællesnævner, og så trækker man blot tællerne fra hinanden:
For at kunne lægge en brøk og et heltal sammen, er vi nødt til at omskrive heltallet til en uægte brøk med samme nævner som brøken. Vi kan eksempelvis være givet opgaven
Heltallet 3 kan altså også skrives som den uægte brøk
For at kunne trække en brøk fra et heltal eller et heltal fra en brøk er vi nødt til at gøre omtrent det samme som for at lægge dem sammen: heltallet skal omskrives til en brøk med samme nævner som brøken. Tag eksempelvis stykket
Og så kan vi gennemføre stykket, som vi ville, når vi trækker to brøker fra hinanden:
Når man ganger brøker, ganger man tæller med tæller og nævner med nævner. Hvis vi eksempelvis har brøkerne
Når man dividerer med brøker, svarer det til, at man ganger på skrå. Det vil altså sige, at man ganger den første brøks tæller med den anden brøks nævner og omvendt. Det ser sådan ud:
Når man ganger en brøk med et heltal, ganger man kun op i tælleren. Nævneren forbliver altså uændret. Her er et eksempel med heltallet 8 og brøken
Her vil det helt klart være en fordel at reducere den resulterende brøk,
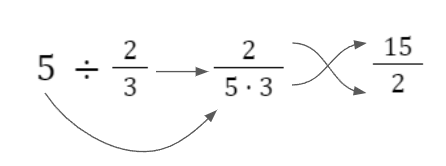
Når vi taler om at dele brøker og heltal, er det vigtigt, at vi lægger mærke til, om vi dividerer en brøk med et heltal, eller om vi dividerer et heltal med en brøk - fremgangsmåden er nemlig forskellig. Når vi har et heltal, vi gerne vil dividere med en brøk, ganger vi brøken ned i nævneren, og så vender vi brøken om: Hvis man derimod dividerer en brøk med et heltal, kan man nøjes med at gange den ned i nævneren:
Nogle gange, når man har regnet med en brøk, får man et resultat, som man kan reducere - altså gøre mindre. Det kan man med brøker, der beskriver en del, som kan skrives mere simpelt og med mindre tal. Man kan se, om det er tilfældet ved at undersøge, om der findes et tal, der går op i både tæller og nævner. Nu tager vi fat i eksemplet fra tidligere, brøken
Nu har vi reduceret brøken, men oftest vil vi gerne reducere brøken så meget som muligt, og denne brøk kan stadig reduceres. Vi kunne reducere med 2 igen, men så ville vi igen stå med en brøk, der kan forkortes yderligere - i stedet reducerer vi med det største tal, der går op i både tæller og nævner, 4:
Den mest reducerede form af
Nu hvor du har fået styr på alle brøkregnereglerne, tager vi lige en hurtig gennemgang af dem på et mere generelt plan: eller skrevet med brøkstreger i stedet for divisionstegn (vi taler om, hvorfor det er det samme i næste afsnit): eller med brøkstreg:
Brøker er bare en måde at udtrykke en del af et hele på. Der er i hvert fald to andre metoder for det, som vi i matematikken bruger ret ofte: procent og decimaltal. Alle tre kan udtrykke de samme dele. Tag eksempelvis en halv. Hvis vi skulle skrive det som en brøk, ville vi skrive det sådan her:
Her går der noget galt. Alt efter om man ganger eller dividerer først, får man to forskellige resultater. Men man skal i princippet gange og dividere samtidig: Hvis man dividerer først, er resultatet 11: Hvis man ganger først, bliver det 3: Her er der altså en fejl i syntaksen, dvs. måden stykket er skrevet op på. Det kan i princippet fixes med parenteser, men ved at skrive divisionen med en brøkstreg i stedet, undgår vi sådan en fejl: Når man skriver stykket sådan, kan det kun tolkes på én måde. Vi har altså kigget på, hvordan brøker er essentielle dele af matematik og bruges til at repræsentere dele af en helhed. Vi har set, hvordan brøker er opbygget af tælleren, brøkstregen og nævneren og kan bruges til at beskrive dele af ting eller af tal. Vi har også set på, hvordan man regner med brøker, og hvordan de kan bruges til at skrive divisionsstykker op. Det er vigtigt at forstå brøker, da de er fundamentale i mange aspekter af matematik og dagligdags liv. Husk, at øvelse gør mester, så jo mere du arbejder med brøker, desto bedre vil du forstå dem. Med en solid forståelse af brøker vil du kunne løse komplekse matematiske problemer og finde brøker nyttige i mange praktiske situationer. Så gå videre og udforsk verden af brøker - det åbner døren til en dybere forståelse af matematikkens fascinerende verden! Øvelse gør mester! Find opgaver med brøker her.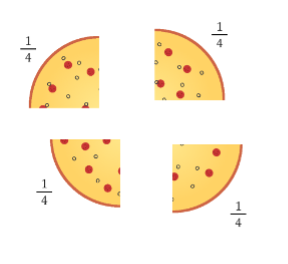
Brøkers størrelser
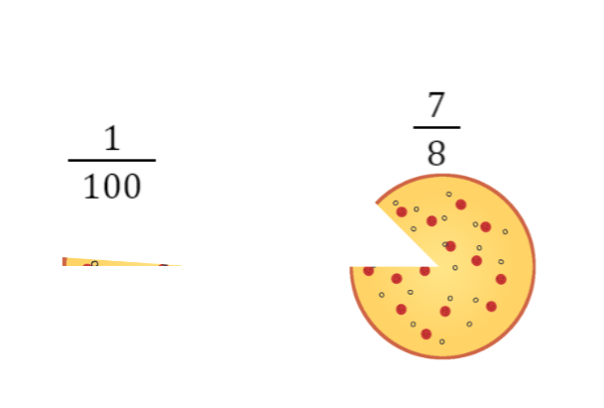
Ægte og uægte brøker
At regne med brøker
At finde fællesnævner
Hvis vi for eksempel har brøkerne
At lægge brøker sammen med brøker
At trække brøker fra hinanden
At lægge brøker og heltal sammen
At trække brøker og heltal fra hinanden
At gange brøker
At dele brøker
At gange brøker og heltal
At dele brøker og heltal
At reducere brøker
Når der er tale om at reducere en brøk mest muligt, vil man også skulle gøre en uægte brøk til en ægte brøk, som vi kiggede på i afsnittet “ægte og uægte brøker”.
Hurtig gennemgang af brøkregnereglerne
Addition med brøker:
Addition med brøk og heltal:
Subtraktion med brøker:
Subtraktion med brøk og heltal:
Multiplikation med brøker:
Multiplikation med heltal og brøker:
Division med brøker:
Et heltal divideret med en brøk:
eller med brøkstreg:
En brøk divideret med et heltal:
Brøker er bare division
I stedet for at se på brøker som dele af et hele, kan man også se på en brøk som et divisionsstykke, der bare venter på at ske. Brøken
Mange foretrækker faktisk at skrive division på den måde, fordi det gør det meget klarere, i hvilken rækkefølge man skal gribe et komplekst regnestykke an! Man kan eksempelvis kigge på følgende stykke:
Brøkernes funktion