Hvad kendetegner en trekant? Og hvad er en trekant i matematik?
“Vinkelsum” betyder, at alle tre vinkler i trekanten skal give 180°, når man lægger dem sammen.
Hvilke forskellige slags (typer) trekanter er der?
Retvinklet trekant
En ret vinkel er en vinkel, som er præcis 90°. De findes overalt, f.eks. har et stykke papir fire rette vinkler i hjørnerne. En retvinklet trekant kan ikke have tre rette vinkler, så den har derfor kun en enkelt ret vinkel.
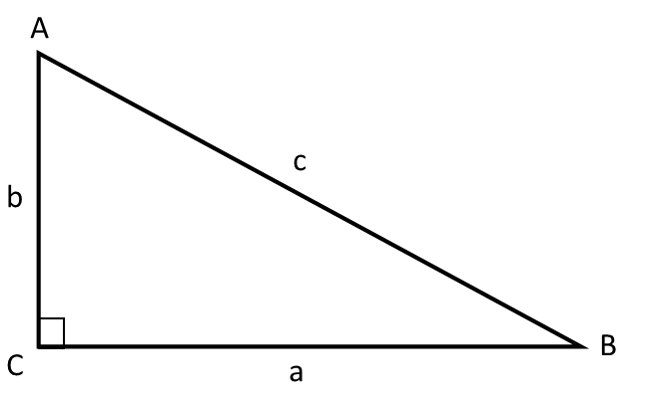
Når man tegner en trekant, så giver man som regel siderne, og vinklerne bogstaver som navne. Vinkler skrives altid med stort, og sider skrives altid med småt, hvor man matcher bogstavet fra vinklen med siden overfor, ligesom på tegningen.
En retvinklet trekant er lidt særlig, da der er nogle specielle regler for den. Det er pga. noget, der hedder Pythagoras, det kommer vi ind på senere i artiklen, lige nu kan vi bare fortælle om reglerne.
Når man tegner en retvinklet trekant, så hedder vinklen med den rette vinkel C. Man kan vise, at vinklen er retvinklet ved at tegne en firkant i den.
I en retvinklet trekant kalder man de to korte sider (a og b) for katete(r) og den lange side for hypotenuse.
Stumpvinklet trekant
En stump vinkel er en vinkel, som er mere end 90°. På samme måde som med den retvinklede, er en stumpvinklet trekant altså en trekant med en stump vinkel. Automatisk bliver de to andre trekanter spidse vinkler, altså vinkler som er under 90°.
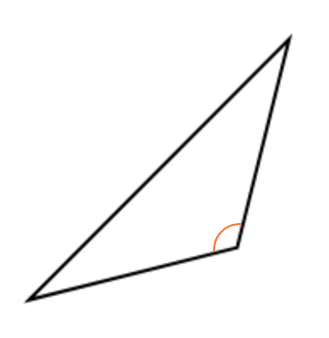
En stump vinkel tegner man ved at lave en bue i vinklen. Her navngiver man også vinklerne og siderne med bogstaver, men der er ikke nogen særlige regler for, hvilke der skal hedde hvad.
Spidsvinklet trekant
En spids vinkel er en vinkel, som er mindre end 90°. Det, der adskiller den her type trekant fra de andre, som har “vinkel” i navnet, har den spidsvinklede trekant udelukkende spidse vinkler, og altså ikke kun en enkelt.
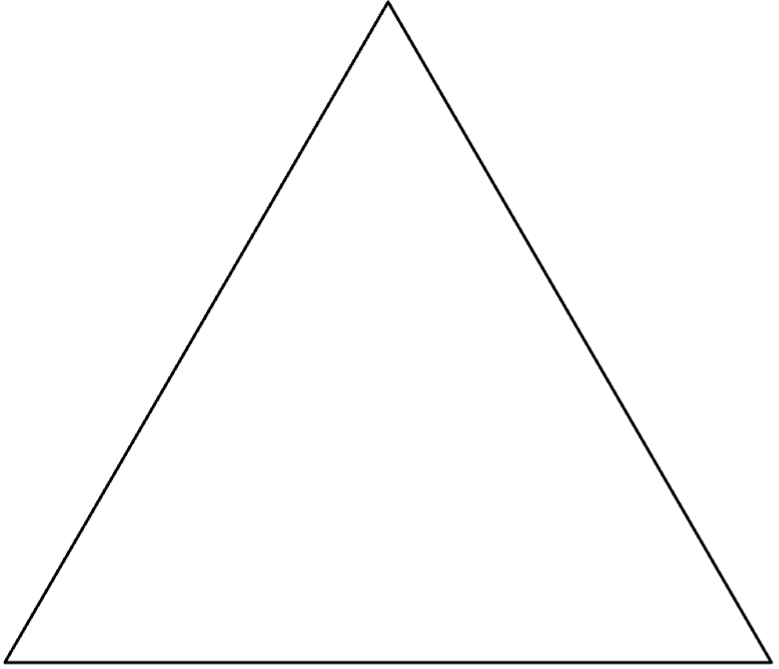
Ligesidet trekant
En ligesidet trekant har tre lige sider, dvs. tre sider, som er lige lange. Derfor bliver vinklerne også lige store og vil altid være 60°, ligegyldig hvor lange siderne er. Trekanten er derfor også en spidsvinklet trekant.
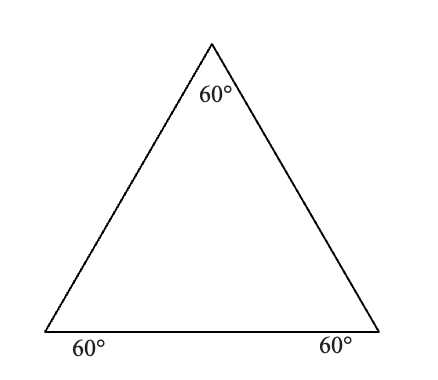
Ligebenet trekant
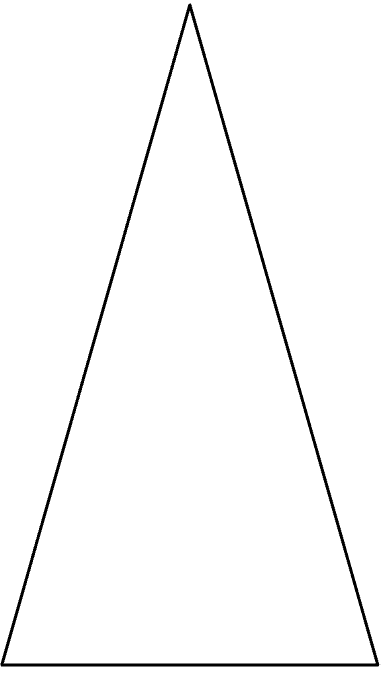
En ligebenet trekant har to ben, som er lige lange. Den kan derfor også være en retvinklet trekant eller en stumpvinklet trekant, afhængig af hvor lange siderne er. De to sider som er lige lange, kalder man ben, hvor den sidste side hedder grundlinjen.
Areal og omkreds
Arealet af en trekant er præcis det halve af arealet af en firkant. Arealet af en firkant er
Hvis vi skal oversætte det til trekant-sprog, så skal vi bruge grundlinje og højde. Når man tager halvdelen af noget, kan man dividere det med 2.
Lad os prøve at skrive vores omskrivning:
Normalt når man skriver formler, så skriver man med bogstaver. Teknisk set kan vi vælge lige de bogstaver, vi vil, men det er rimelig nærliggende at bruge forbogstaverne i ordene, altså h og g.
Omkredsen af en trekant er de tre sider lagt sammen. Hvis vi skal skrive det som en formel, kan vi kalde siderne for s1, s2 og s3.
Pythagoras
Pythagoras’ læresætning (typisk bare kaldet Pythagoras) er en formel, man bruger til at regne ud, hvor lange siderne i en retvinklet trekant er. Det kan f.eks. være relevant, hvis man vil finde omkredsen af en trekant, men ikke ved hvor lang en af siderne er. Det er vigtigt at huske, at den kun kan bruges med retvinklede trekanter, ellers vil den ikke virke.
Pythagoras-formlen er:
Som der står tidligere i artiklen under “Retvinklet trekant”, så har siderne bogstaver som navne. Særligt er det vigtigt at huske, at den lange side hedder c – og på matematiksprog kalder man den også for hypotenusen. De to korte sider, kateterne, hedder a og b – og der er ikke nogen regler for, hvilken der er hvilken, man kalder bare den ene for a og den anden for b.
Lad os regne med et eksempel.
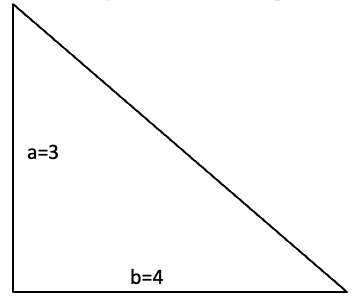
I den her får vi at vide, at side a er 3 og b er 4. Lad os prøve at sætte det ind i Pythagoras:
Nu skal den løses, ligesom man ville løse en ligning. Først regner vi venstresiden ud:
Nu skal vi fjerne potenstallet fra højresiden. Det modsatte af potens er rod, og da potensen er 2, skal vi tage kvadratroden. Kvadratroden af 25 er 5, altså får vi vores svar:
Og sådan har vi fundet hypotenusens længde. Nogle gange er det en af kateterne, man skal regne ud, men så bruger man stadig Pythagoras, sætter tallene ind på deres plads, og løser det som en ligning.
Opsummering
Har du styr på de forskellige slags trekanter? Føler du dig tryg i at finde arealet og omkredsen af en trekant? Hvad med sidelængderne i en retvinklet trekant? Har du lært at stave til Pythagoras?sym