Retningsvektor – en guide til at forstå, hvad det er

Hvad er en vektor?

En vektor er et objekt, som har en længde og en retning. Den vil oftest være betegnet ved små bogstaver med pil over. Et eksempel på dette kan være $\stackrel{\to <!--\; \to \; -->}{a}$ Koordinaterne for en vektor skriver man i en høj parentes således: $\stackrel{\to <!--\; \to \; -->}{a}=\left(\begin{array}{c}{a}_1\\ a_2\end{array}\right)$

En vektor illustreres som en pil, og kan flyttes rundt i et koordinatsystem, så længe den bibeholder samme længde og retning.

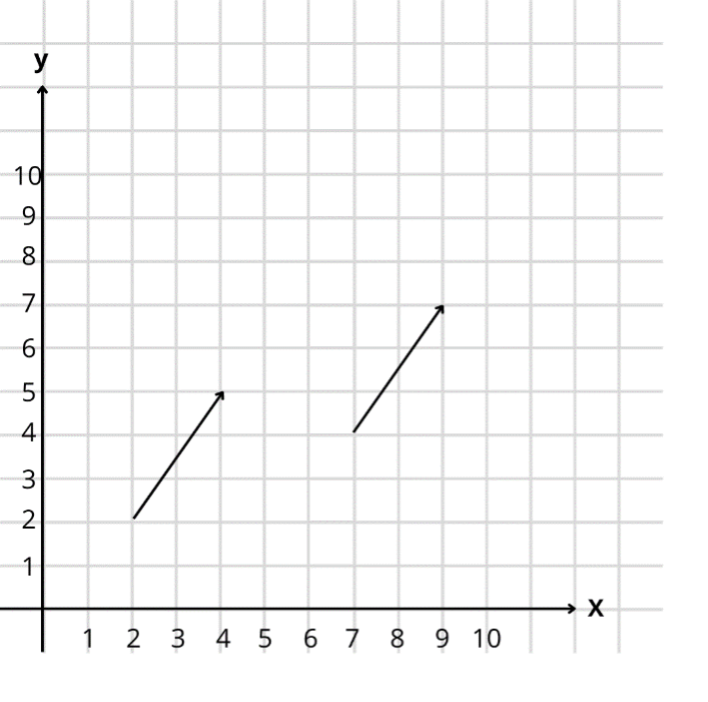
Her kan vi se vektoren $\stackrel{\to <!--\; \to \; -->}{a}$ placeret to forskellige steder i vores koordinatsystem. Grunden til, at begge kan betegnes som $\stackrel{\to <!--\; \to \; -->}{a}$ , er da de har samme længde og retning. Man finder koordinatsættet til en vektor således:

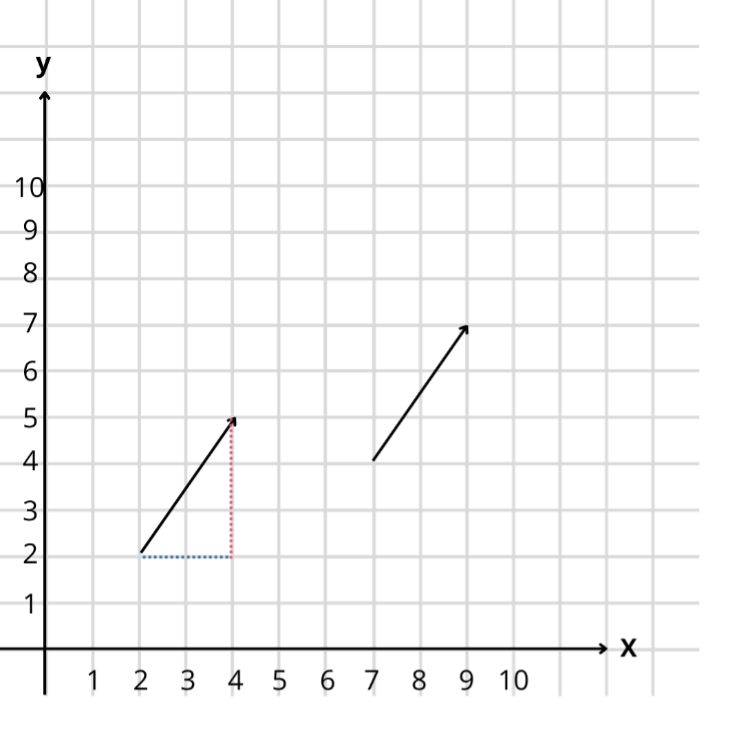
Man begynder ved piles start, og bevæger sig i den retning, som pilen fører hen. Først finder vi koordinaten til $a_1$ ved at se, hvor meget vi skal gå ud vandret. Her hjælper den blå stiplede linje os med at forstå dette.
Vi kan se, at man her skal gå 2 ud, og det er dermed koordinaten til $a_1$.

Nu finder vi koordinaten til $a_2$, ved at se, hvor meget vi skal gå op eller ned lodret.
Her hjælper den røde stiplede linje os.
Vi kan se, at man her skal gå 3 op, og det er dermed koordinaten til $a_2$.

Koordinatsættet til vektoren $\stackrel{\to <!--\; \to \; -->}{a}$ på billedet bliver dermed $\stackrel{\to <!--\; \to \; -->}{\mathrm{a}}=\left(\begin{array}{c}2\\ 3\end{array}\right)$

Nu, hvor vi er blevet lidt klogere på, hvad en vektor er, kan vi kigge nærmere på, hvad en retningsvektor er.

Hvad er en retningsvektor?

En retningsvektor er en vektor, som er ret med en linje, og derfor også parallel med en linje. En retningsvektor betegnes ved et lille r med en pil over, $\stackrel{\to <!--\; \to \; -->}{r}$.

Koordinaterne for en retningsvektor skriver man også i en høj parentes således $\stackrel{\to <!--\; \to \; -->}{r}=\left(\begin{array}{c}{r}_1\\ r_2\end{array}\right)$.

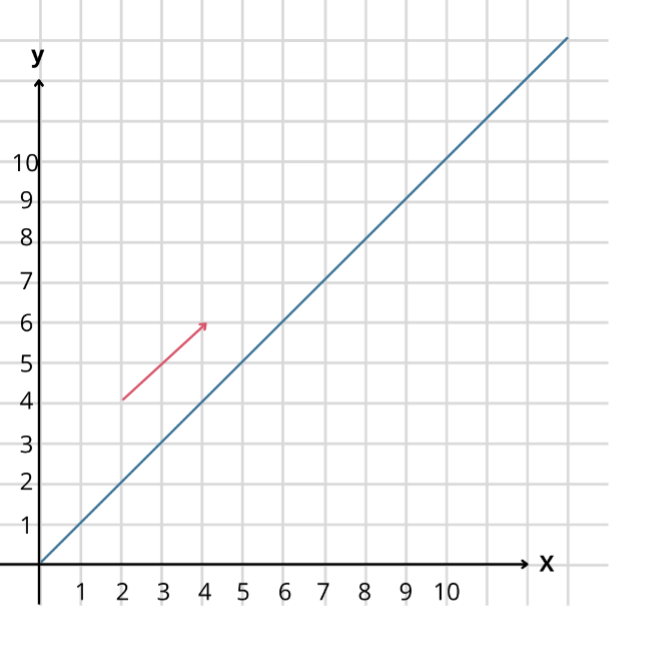
Her ses retningsvektoren $\stackrel{\to <!--\; \to \; -->}{\mathrm{r}}=\left(\begin{array}{c}2\\ 2\end{array}\right)$ for den blå linje. Grunden til, at denne vektor er retningsvektor for linjen, er da den er parallel med linjen.

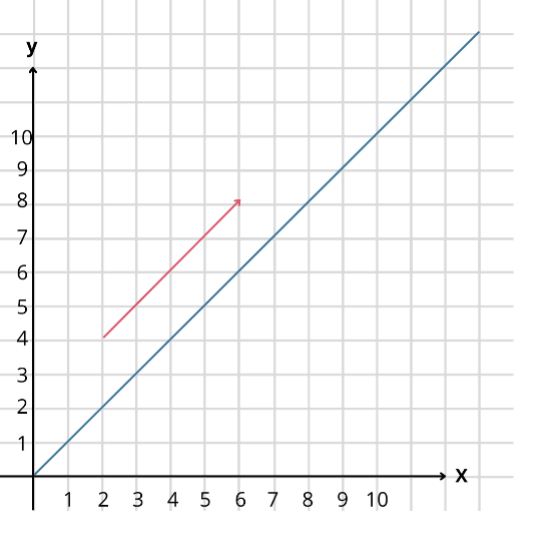
Her ses retningsvektoren $\stackrel{\to <!--\; \to \; -->}{\mathrm{r}}=\left(\begin{array}{c}4\\ 4\end{array}\right)$ for den blå linje. Grunden til, at denne vektor stadig er retningsvektor for linjen, er da den også stadig er parallel med linjen.
Den har samme retning som linjen, og er blot blevet længere.

Jeg håber, at du nu har bedre styr på retningsvektorer, og har mod på, at arbejde videre med dem. God fornøjelse!