Vi kigger på kvadratsætninger - hvordan løser man (a + b)²?

Vær med, når vi springer ud i kvadratsætningerne og lær både, hvad de er for en størrelse, hvordan man bruger dem, og hvorfor det hedder, som de gør!

Hvad er kvadratsætninger?

Kvadratsætningerne er en samling regneregler, vi bruger til at ophæve parenteser. Helt konkret bruger vi dem, når en parentes er sat i anden. De tre kvadratsætninger er:

$(a + b)^{2} = a^{2} + b^{2} + 2 a b$

$(a - b)^{2} = a^{2} + b^{2} - 2 a b$

$(a + b) (a - b) = a^{2} - b^{2}$

Dem gennemgår vi én efter én og ser, hvordan vi kommer frem til dem.

Den positive kvadratsætning

Når vi har udtrykket $(a + b)^{2}$ , og vi gerne vil ophæve parentesen, så er det vigtigt, vi ved, at når vi sætter noget i anden, svarer det til at gange det med sig selv. Altså må udtrykket $(a + b)^{2}$ kunne omformuleres til $(a + b) * (a + b)$ . Her kan vi gange hvert led med hinanden, for så at få det forlængede udtryk $a^{2} + b^{2} + 2 a b$ . Det kan godt være rigtig svært at se, hvorfor vi kan det.

Vi kan derfor vælge at se udtrykket som et kvadrat, som vi gerne vil beregne arealet af.

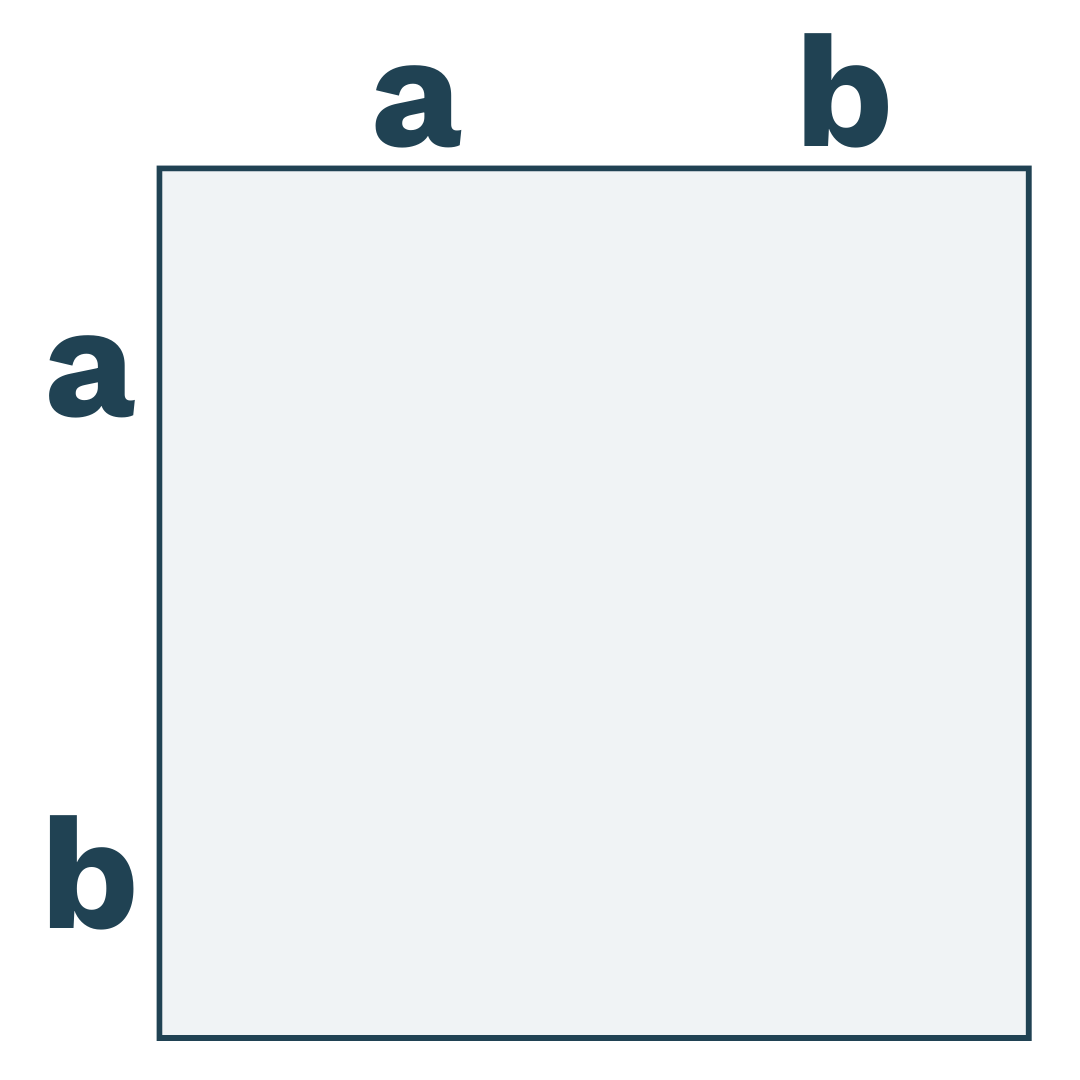
Så kan vi inddele kvadratet i 2 kvadrater og 2 rektangler:

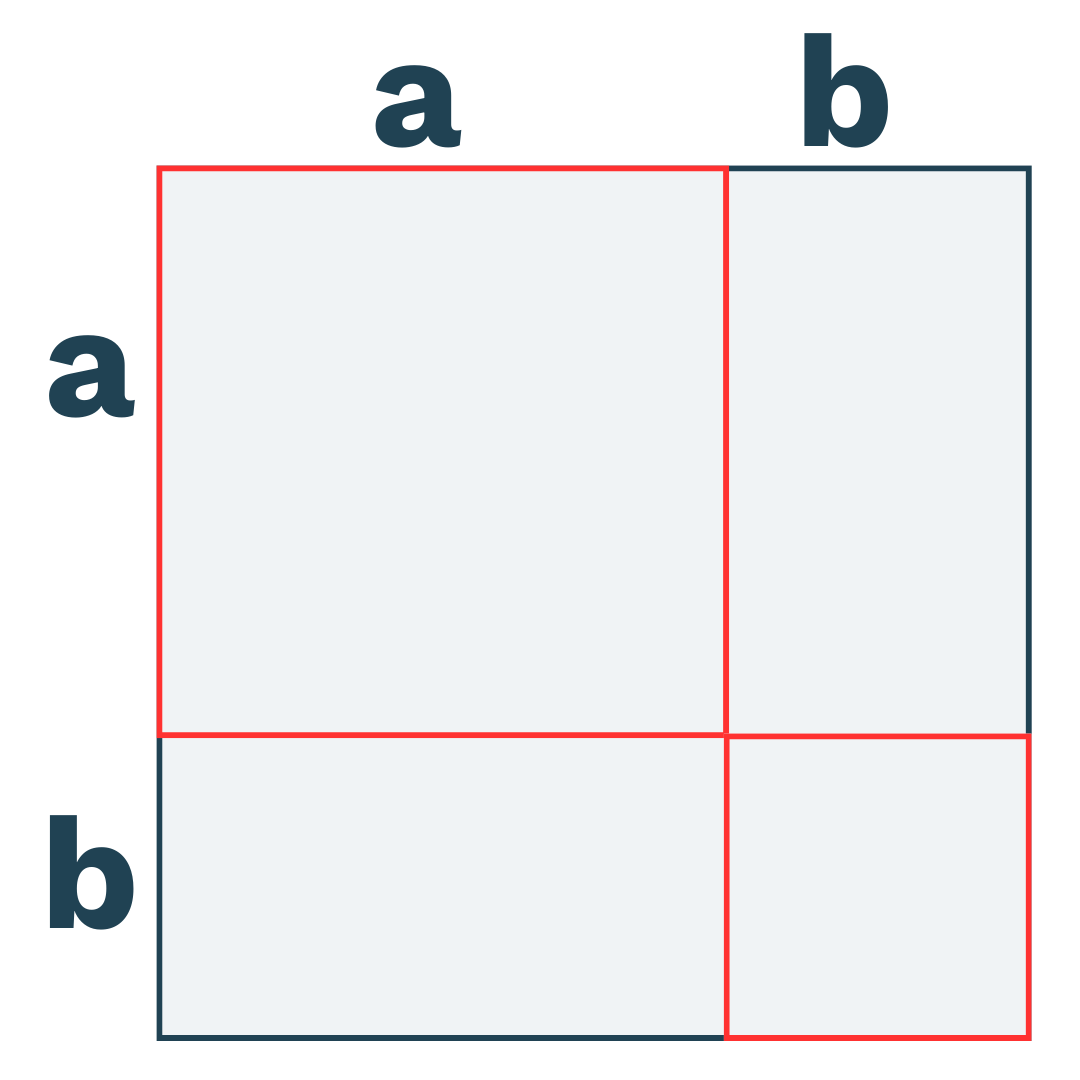
Vi kan så beregne arealet af de mindre firkanter:

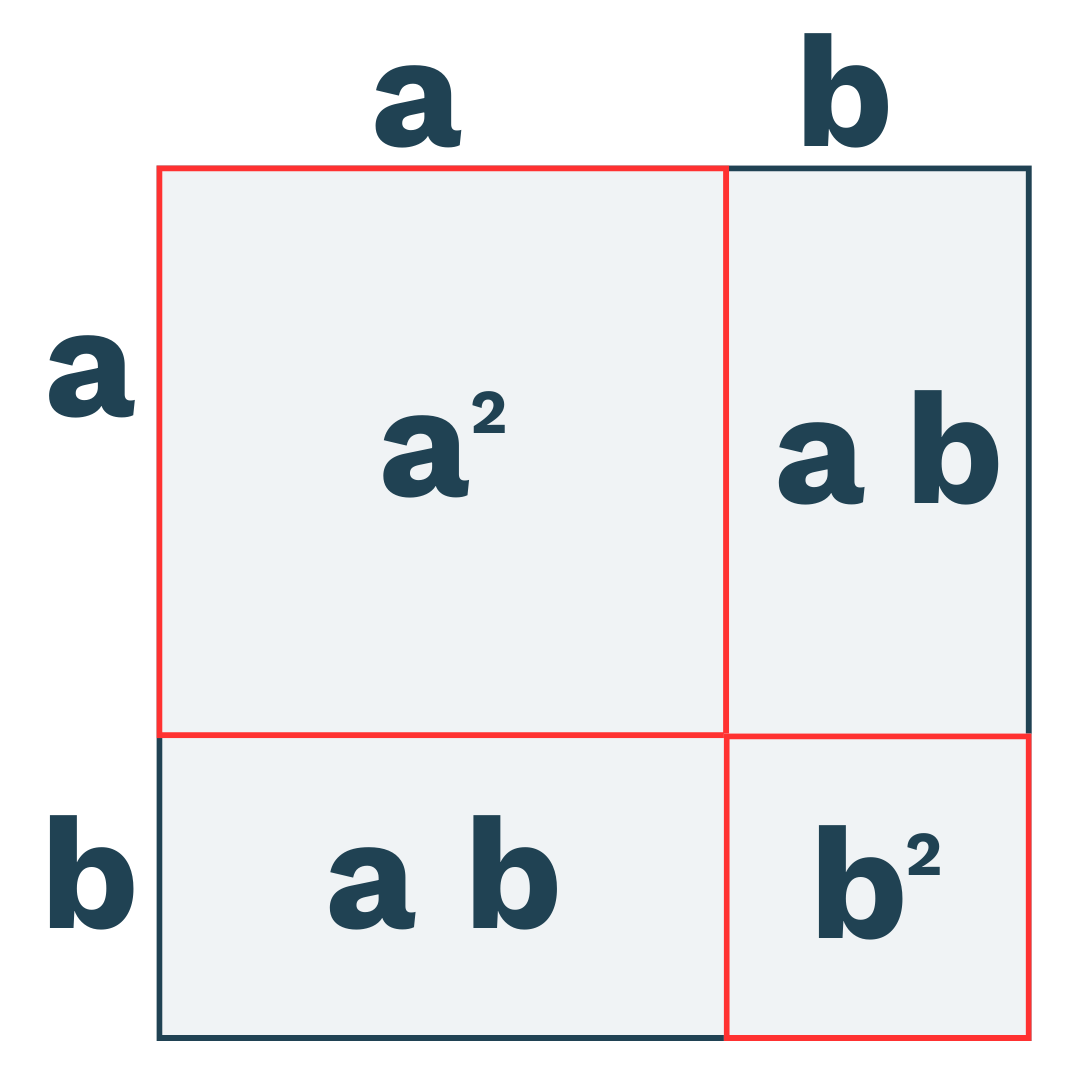
Hvis vi så lægger arealet af de fire firkanter sammen, så får vi arealet af det store kvadrat:

$A = a^{2} + b^{2} + a b + a b = a^{2} + b^{2} + 2 a b$

Altså er $(a + b)^{2} = a^{2} + b^{2} + 2 a b$

Den negative kvadratsætning

På samme måde kan vi gribe $(a - b)^{2}$ an. Vi tegner et kvadrat:

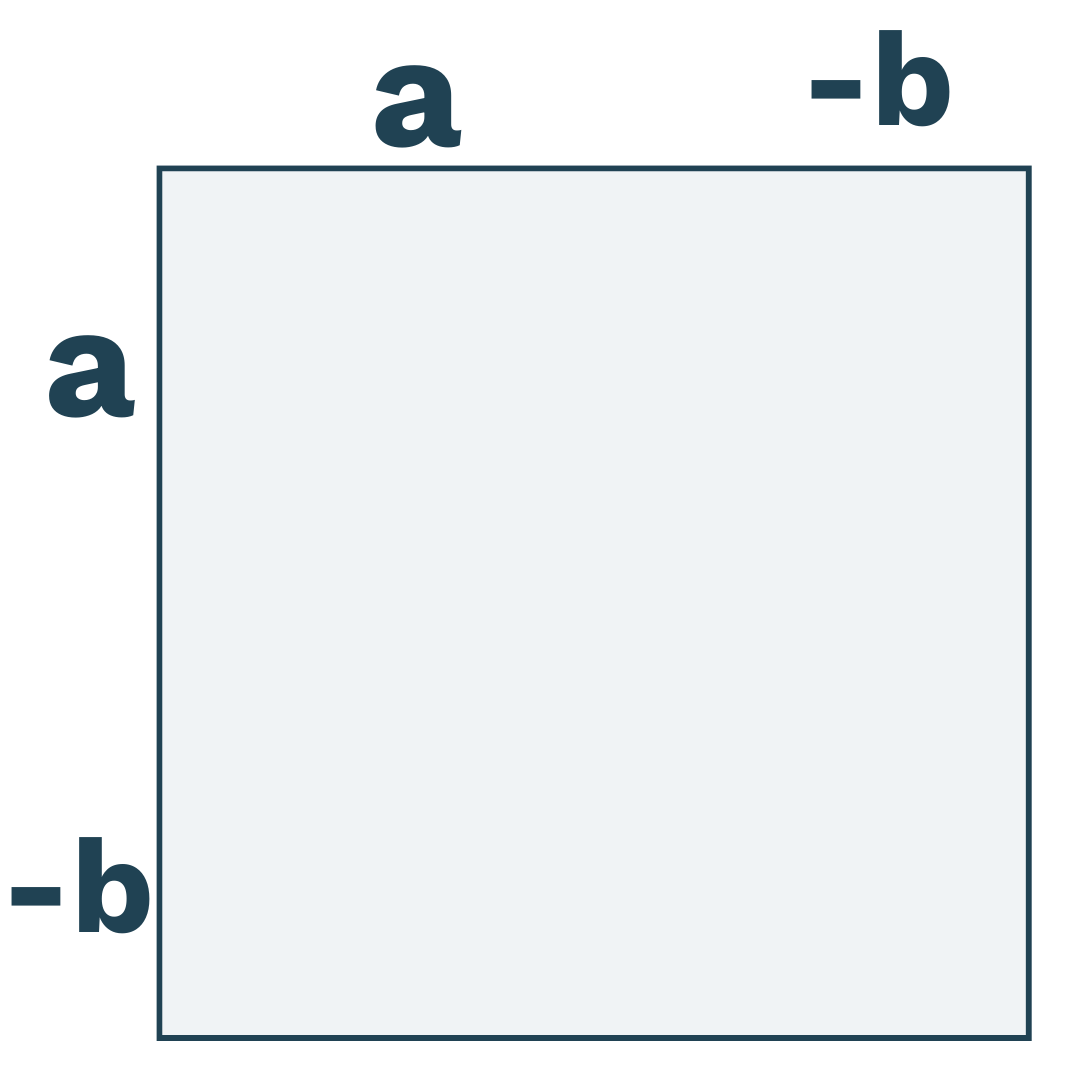
Det kan vi også inddele i mindre firkanter og finde arealet af hver af dem. Her er det vigtigt at bemærke, at når vi ganger minus med minus, så får vi plus, og derfor er $(- b) * (- b) = b^{2}$ :

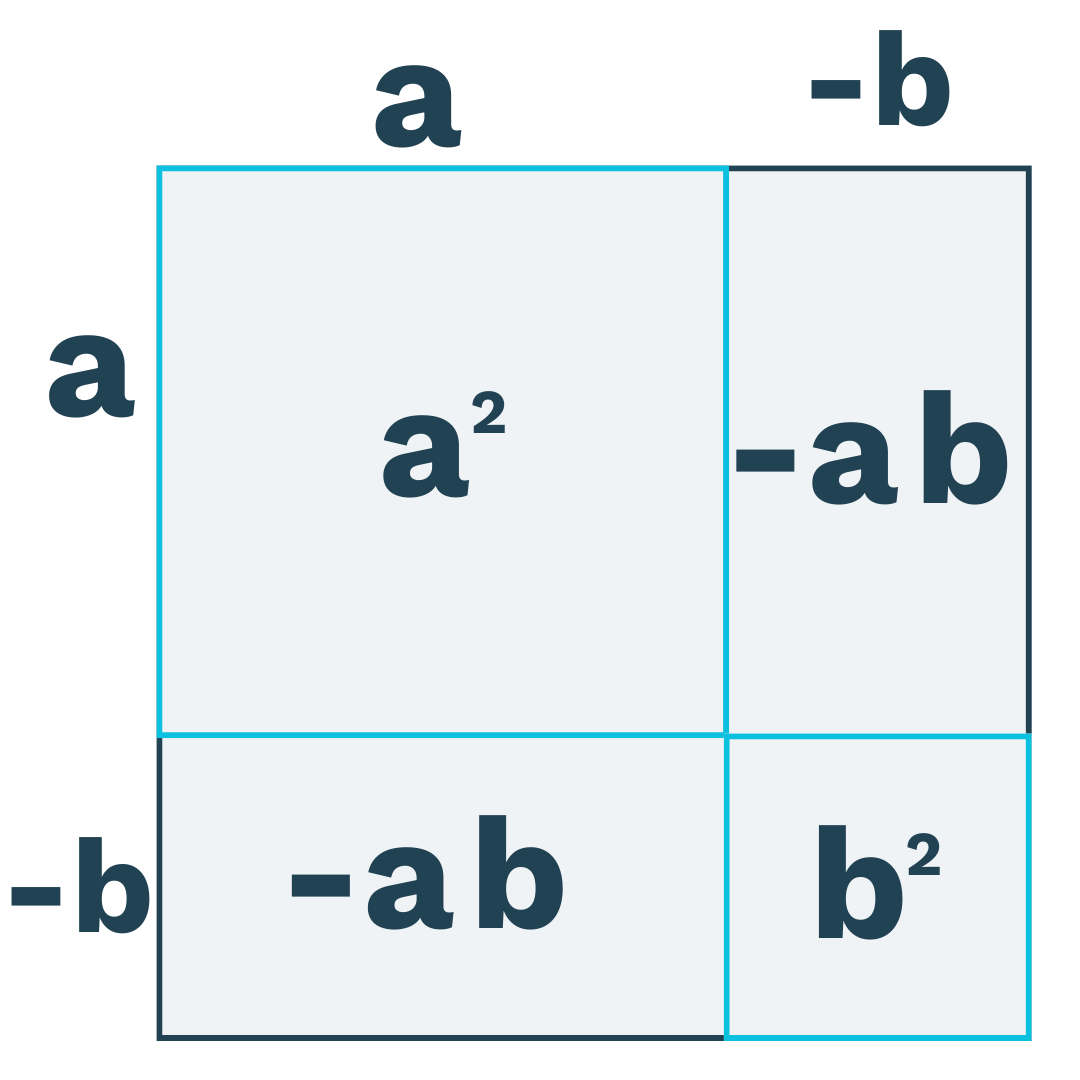
Så lægger vi de fire firkanter sammen:

$a^{2} + b^{2} - a b - a b = a^{2} + b^{2} - 2 a b$

Altså er den negative kvadratsætning:

$(a - b)^{2} = a^{2} + b^{2} - 2 a b$

Den blandede kvadratsætning

Den tredje kvadratsætning som vi kigger på, adskiller sig lidt fra de to andre, fordi den ikke består af ét udtryk sat i anden, men af to udtryk der ligner hinanden, som vi ganger sammen. De to udtryk lyder:

$(a + b) (a - b)$

Vi kan gribe dem an på samme måde som vi har gjort med de 2 tidligere. Vi skriver dem op som længderne på en firkant. Nu er vores firkant ikke et kvadrat mere, fordi den ene side er $(a + b)$ lang, og den anden er $(a - b)$ lang:

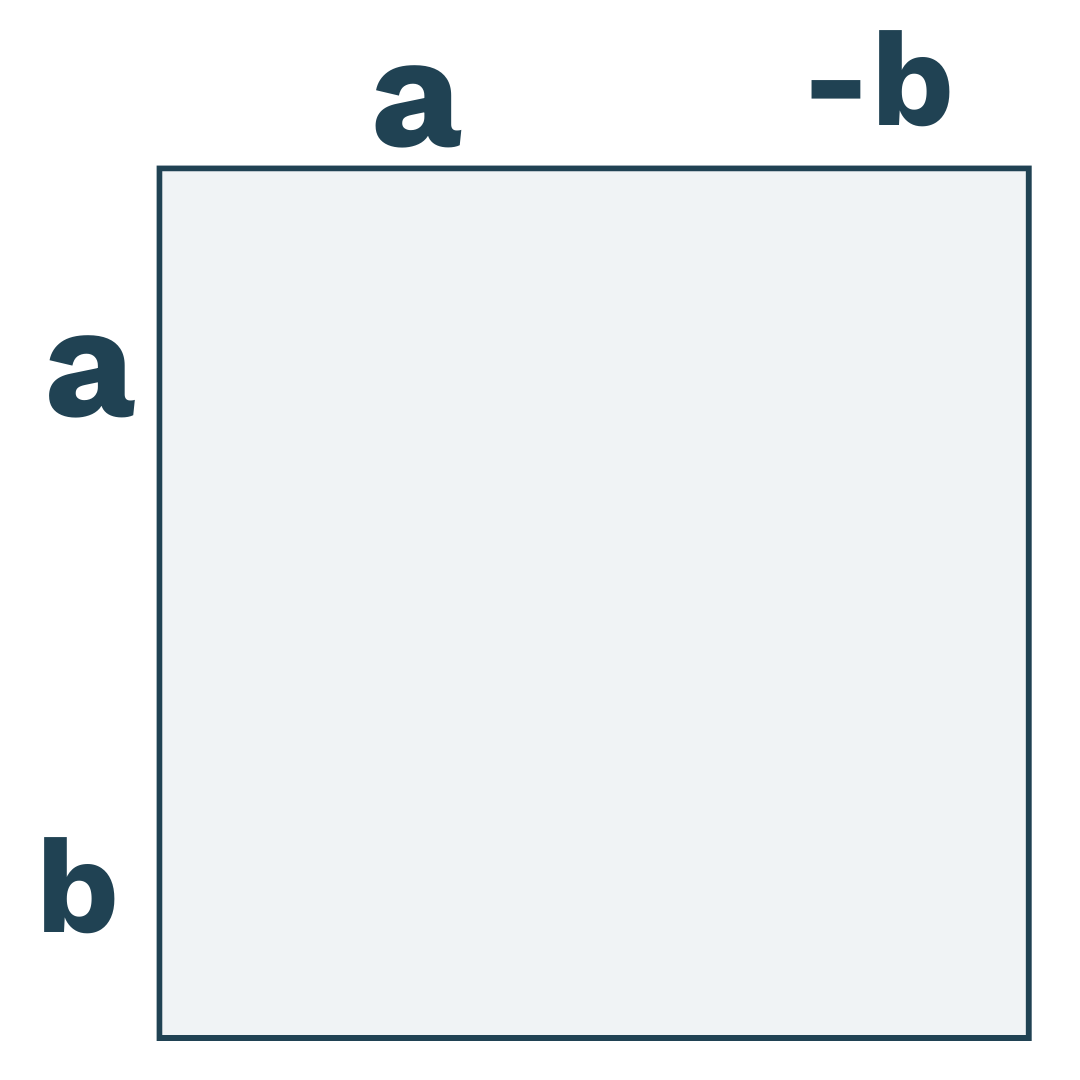
Vi kan dele firkanten op i ét kvadrat og tre rektangler og beregne arealet af dem:

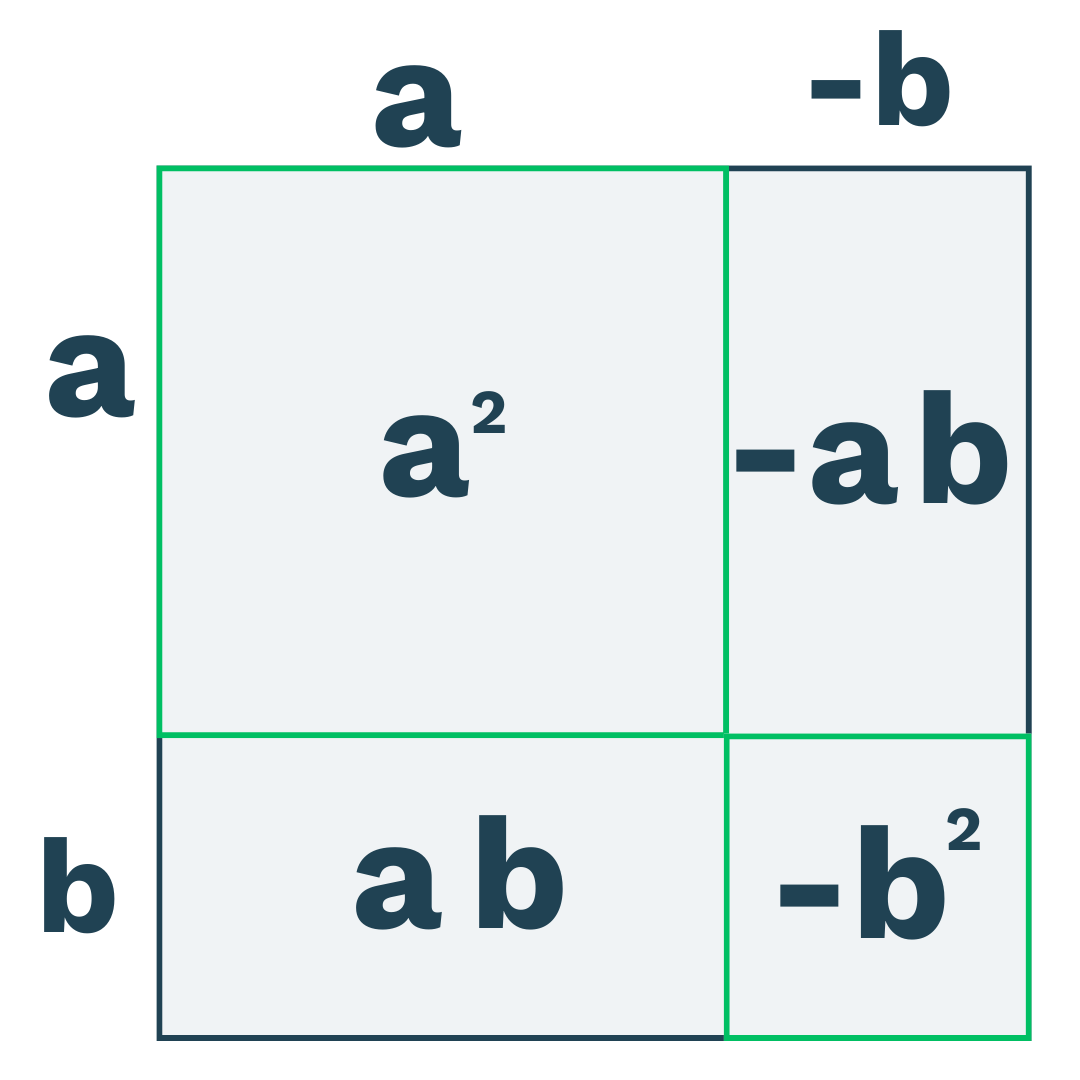
Og så lægger vi dem sammen:

$a^{2} - b^{2} + a b - a b = a^{2} - b^{2}$

Altså må den blandede kvadratsætning være:

$(a + b) (a - b) = a^{2} - b^{2}$

Regneeksempler

Eksempel 1: den positive

Opgave: reducér udtrykket $i * h + (h + i)^{2} + c$ mest muligt.
Vi starter med at bruge kvadratsætningen til at pakke parentesen ud:

$i * h + h^{2} + i^{2} + 2 h i + c$

Så kan vi lægge i h og h i sammen, og dermed får vi:

$h^{2} + i^{2} + 3 h i + c$

Og nu kan vi ikke reducere udtrykket yderligere, og vi må derfor være færdige.

Eksempel 2: den negative

Opgave: reducér udtrykket $(p - g)^{2} - g + p$

Vi bruger kvadratsætningen til at pakke parentesen ud:

$p^{2} + g^{2} - 2 p g - g + p$

Og der er ikke nogen led vi kan regne yderligere på, og vi er derfor i mål.

Eksempel 3: den blandede

Opgave reducér udtrykket $(h - j) (j + h) + (h * j)$

Vi starter med at bruge den blandede kvadratsætning:

$h^{2} - j^{2} + (h * j)$

Bagefter ophæver vi parentesen:

$h^{2} - j^{2} + h j$

Det kan vi ikke reducere yderligere, så vi er altså i mål.

Du kan dykke dybere ned i kvadratsætninger i denne video fra Restudy. Her fortælles om de 3 kvadratsætninger, der er vigtige at have med, og som bl.a. skal bruges i gennemgangen af 2. gradsligninger.

Find flere videoer på Restudy.dk.

Vi kigger på kvadratsætninger - hvordan løser man (a + b)2?

Vi kigger på kvadratsætninger - hvordan løser man (a + b)²?