Kvadratroden: En af matematikkens vigtigste rødder?

Kvadratrødder - hvad er det egentlig for en størrelse?

Når man tager kvadratroden af et tal, finder man det andet tal, som skal ganges med sig selv, for at man får det første tal. Det kaldes en kvadratrod, fordi hvis det første tal er arealet af et kvadrat, så er det andet tal sidelængden på samme kvadrat.

Hvis vi kalder det første tal A og det andet s, så kan vi illustrere det sådan her:

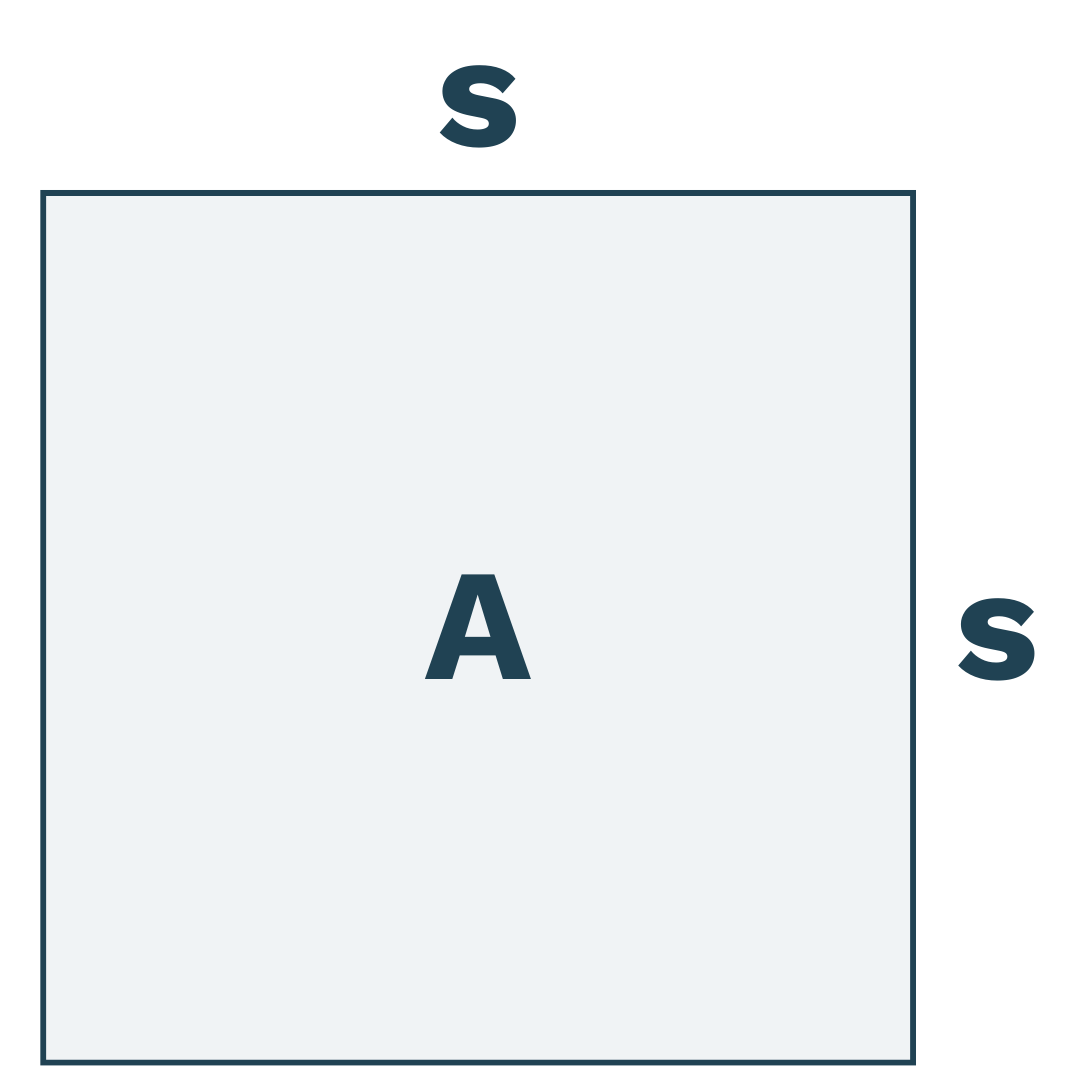
Eller hvis vi skal prøve at gøre det med tal, kan vi bruge 4 som A og 2 som s. Det kan vi, fordi 2 er kvadratroden af 4:

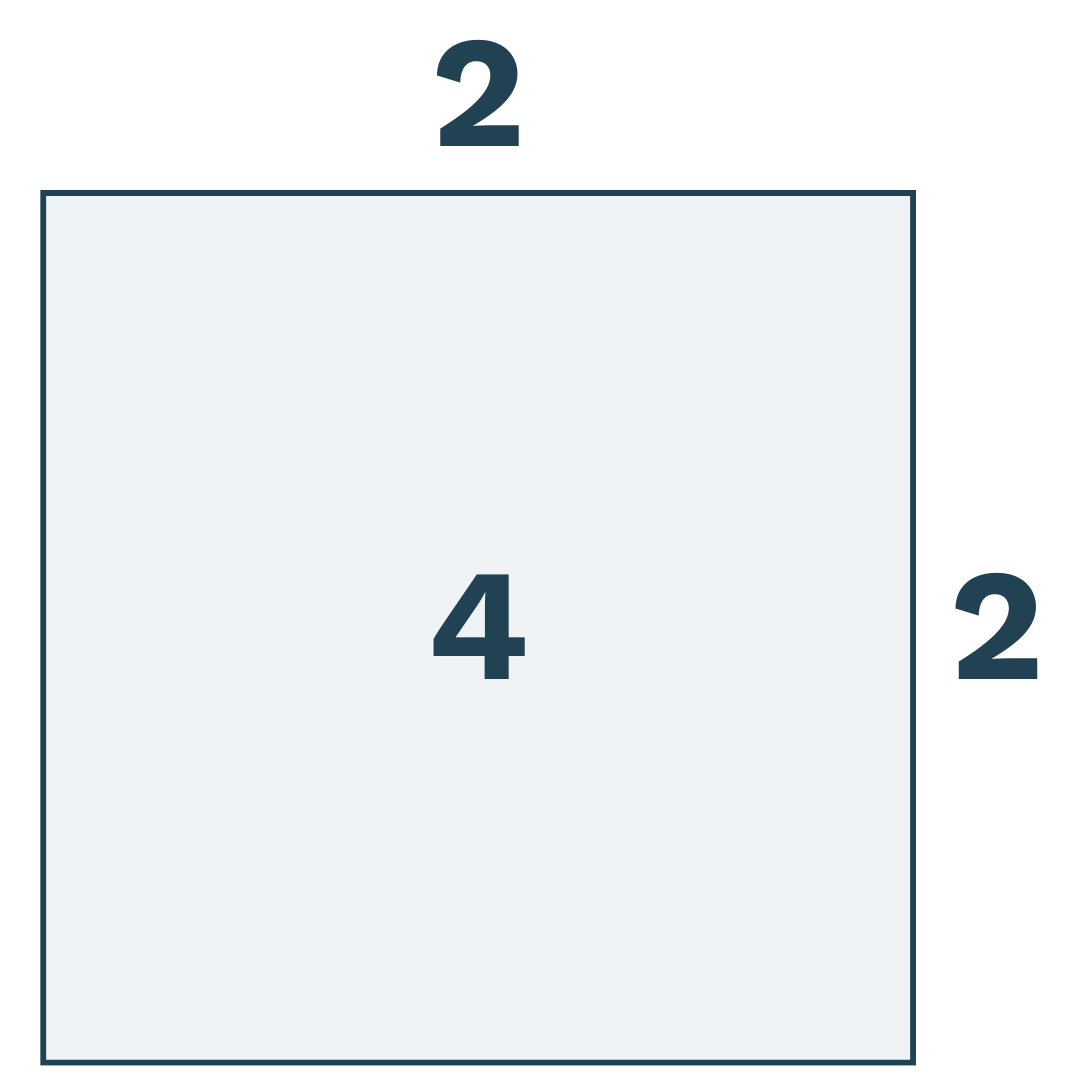
Hvordan skriver man kvadratrødder?

Når vi skriver kvadratrødderne op i matematikken, bruger vi et tegn,
der ser sådan her ud: $\sqrt{\mathrm{X}}$
Inde i tegnet skriver vi det tal, vi gerne vil finde kvadratroden af.
Det kan se sådan her ud: $\sqrt{4}$

Til tider kan der også stå andre ting, der skal beregnes først, inden vi kan tage kvadratroden. Her er et eksempel: Hvis der står $\sqrt{2*2+5}$, er vi nødt til at beregne det inde i kvadratroden. Vi ganger først: $\sqrt{4+5}$ Så lægger vi sammen: $\sqrt{9}$ Og til sidst kan vi så tage kvadratroden: $\sqrt{9}=3$

Typiske kvadrattal

Der er en samling tal, som vi oftere tager kvadratroden af end andre tal. Det er tal, hvis kvadratrødder er hele tal. De er nedenfor:

	1	4	9	16	25	36	49	64	81	100	121	144
$\sqrt{}$	1	2	3	4	5	6	7	8	9	10	11	12

Man kan bruge de typiske kvadrattal til at prøve at nærme sig de mere drilske kvadratrødder. Hvis vi tager udgangspunkt i tallet 21.
De typiske kvadrattal 21 lægger sig mellem, er 16 og 25. Deres kvadratrødder er 4 og 5.

Derfor må $\sqrt{21}$ også lægge sig mellem de to. Vi kan dobbelttjekke ved at taste det ind på en lommeregner. Når vi gør det, får vi at $\sqrt{21}=\mathrm{4,58257569}$. Vi havde altså ret i, at resultatet lå mellem 4 og 5.

Kvadratrødder og potenser

Som du måske har regnet ud i løbet af artiklen, så er kvadratroden det modsatte af at sætte noget i anden. Fordi $2^2=4$ så er $\sqrt{4}=2$.
Det er definitionen af kvadratrødder!
Men hvad så med når man sætter noget i tredje? Hvis man gerne vil kende, hvilket tal man skal gange med sig selv 3 gange for et bestemt tal, så skal man bruge den tredje rod.

Den skriver vi sådan her: $\sqrt[3]{\mathrm{X}}$
- prøv at se om du kan beregne hvad $\sqrt[3]{27}$ er. Vi kan faktisk fortsætte dette system: hvis man tager den fjerde rod af et tal, finder man et tal, som skal sættes i fjerde, og så videre.

Kvadratrødder og negative tal

Når man tager et negativt tal og sætter i anden, så holder tallet op med at være negativt.
Det komplicerer tingene, for med den viden kan vi ikke vide om $\sqrt{4}$ er 2 eller (-2), da de begge tal sat i anden er 4.
Derfor skal vi, når vi regner med kvadratrødder, gøre 1 af 2 ting: For det første kan vi vælge at vise, at der slet ikke kan være tale om et minus-tal. Det kan være når man kigger på for eksempel længder og geometri. Længder kan netop ikke være negative! Noget kan ikke være (-5) cm langt.
For det andet kan vi blive nødt til at skrive at $\sqrt{16}$ er lig 4 ELLER (-4).

Regneeksempler på kvadratrod

Eksempel 1

Opgave: Find kvadratroden af 16.

Eksempel 1 Opgave: Find kvadratroden af 16. Når vi skal finde kvadratroden af 16, kan vi enten A) slå op i vores tabel for typiske kvadrattal og se, om den forekommer, eller B) taste $\sqrt{16}$ ind i vores lommeregner. I tabellen står der 4. Er der nogen grund til, at det ikke også er (-4)? Hvorfor/hvorfor ikke?

Eksempel 2

Opgave: Brug de typiske kvadrattal til at estimere kvadratroden af 50.

For at estimere kvadratroden af 50 finder vi først det nærmeste typiske kvadrattal, der er mindre end 50. Ved at slå op i vores tabel, finder vi ud af, at det er 49. Vi gentager, men finder nu det første typiske kvadrattal, der er større end 50. Det kan vi se er 64. Altså må kvadratroden af 50 være et sted mellem 7 og 8. Kan du regne ud, om det er tættest på 7 eller 8? Hvordan kan du regne det ud?

Eksempel 3

Opgave: Er der forskel på stykkerne $\sqrt{9}+\sqrt{16}$ og $\sqrt{9+16}$ ?

Vi starter med at beregne det venstre af de to stykker. Vi bruger vores tabel til at finde kvadratroden af både 9 og 16, og dem kan vi blot lægge sammen:

$\sqrt{9}+\sqrt{16}=3+4=7$

I det højre stykke er vi nødt til først at finde summen af 9 og 16 og så tage kvadratroden af det resulterende:

$\sqrt{9+16}=\sqrt{25}=5$

Der er altså forskel på de to resultater.
Havde det været anderledes, hvis stykkerne var $\sqrt{9}*\sqrt{16}$ og $\sqrt{9+16}$?
Hvorfor?