Hvad er integralregning, og hvad bruger vi det til?
Hvis vi husker tilbage til differentialregning, mindes vi, at det bruges til at bestemme tangenthældninger, noget om væksthastigheder og optimering. Du kan forestille dig, at integralregning er den omvendte tvilling til differentialregning.
Vi bruger integralregning til at finde arealet under kurven for en funktion, og volumen af et omdrejningslegeme.
Figur 1: Finder areal under kurve fra a -> b.
Når vi finder den afledte funktion, altså f'(x) , kan vi finde vores oprindelige funktion f(x), ved at integrere funktionen. Se figur herunder:
Figur 2: Sammenhæng mellem differentialregning og integralregning
Stamfunktioner
Lad os starte med at se på definitionen for, hvad en stamfunktion er:
Funktionen F(x) kaldes en stamfunktion til f(x), hvis
Vær her opmærksom på, at der er forskel på at skrive med små og store bogstaver i matematik. Ifølge definitionen, er det derfor muligt at undersøge, om en funktion er en stamfunktion til en anden funktion, ved at integrere funktionen - dette kaldes integrationsprøven. Herunder laver vi et eksempel:
Eksempel 1:
Vi betragter funktionen , og ønsker at undersøge om den er en stamfunktion til . Vi differentierer derfor funktionen F(x):
Vi kan nu konkludere, at funktionen F(x) er en stamfunktion til f(x), da
Funktionen
er sågar også en stamfunktion til f(x), da
. Det er altså muligt at lave uendeligt mange stamfunktioner.
Stamfunktion F(x) & G(x) er begge stamfunktioner til f(x), kun med den ene forskel, at deres sidste led, altså konstanten, er forskellig fra hinanden, vi kalder denne konstant for k, og kan nu opstille en alsidig stamfunktion med en variabel konstant:
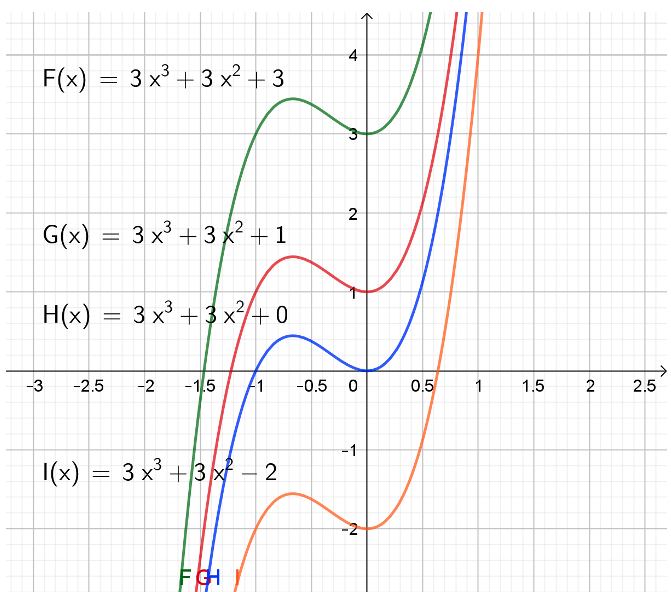
Figur 3: 4 forskellige stamfunktioner ved lodret parallelforskydning
Ubestemte integraler
Vi ved nu hvordan vi går fra F(x) til f(x), men hvordan kommer vi fra f(x) til F(x)?
Der er en helt specifik måde at angive, at en funktion er en stamfunktion til en anden funktion. I vores tilfælde ser vi på
, som er en stamfunktion til
,
her bruger vi notationen:
Heraf læses
som det ubestemte integral af
. Det langstrakte s, altså
, kaldes et integraltegn, og
kaldes integranden.
Det sidste udtryk dx er en måde at sige, vi er færdige, og x’et betyder, at x er variablen i udtrykket. Vi kan nu opskrive en definition for ubestemte integraler:
Hvis F(x) er en stamfunktion til f(x), kan vi konkludere, at
.
Ved at sammenfatte denne definition og den forrige, kan vi bestemme, at:
kaldes det ubestemte integral af f(x), og f(x) kaldes for integranden.
Når vi finder stamfunktionen vha. integration, siger vi, at vi integrerer.
Lad os herunder se på et eksempel:
Vi ønsker at integrerer funktionen
, hvilket vi skriver op herunder:
For at integrere , benytter vi formel 137 i UVM’s matematik A formelsamling, se link i bunden af artiklen.
Vi kan nu opskrive integralet:
Vi skriver "+k", da vi her betragter det ubestemte integral af - se figur 3.
Arealet under graf og bestemte integraler
Vi husker fra ubestemte integraler, at 2 stamfunktioner kun afviger med en konstant, k. Det betyder altså, at vi kan lave uendelige mange stamfunktioner til en funktion . Som det ligger i ordet, så er stamfunktioner en funktion. Nu vil vi kigge på bestemte integraler, og hvordan man kan beregne arealet under en graf.
Bestemte integraler bestemmer et tal mellem 2 punkter, fx a og b, se figur 1. Formlen til at finde det bestemte integral af en funktion finder vi på side 21, formel 147 i formelsamlingen, som lyder:
Hvor F(x) er en stamfunktion til f(x).
Her kaldes a den nedre grænse og b den øvre grænse. Vær opmærksom på notationen med klammer om stamfunktionen, da det trækker ned til skriftlig matematik, hvis man ikke husker
.
Tallet
kaldes det bestemte integral af
i
Vi ved nu, hvordan man finder bestemte integraler, det er derfor muligt at finde arealet under grafen. Se figur 4 herunder, hvor vi kigger på funktionen hvor arealet er fundet mellem og
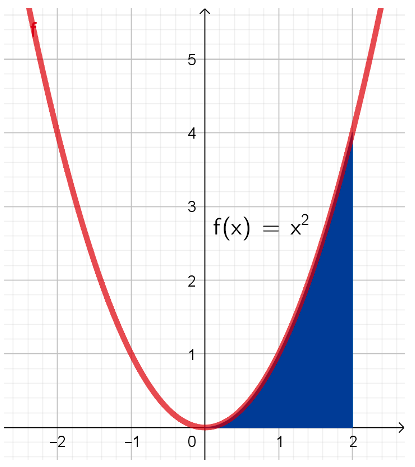
Figur 4: Graf og x^2, og markering af areal mellem [0;2]
For at bestemme arealet, bruger vi nu formel 153, hvilket er en forkortet formel version af formel 147.
Inden vi kan beregne arealet, må vi finde stamfunktionen for
Nu beregner vi arealet for figur 4:
Vi kan nu konkludere, at arealet er 2,67
I matematik er der ofte et lille men, hvilket der også er her. Hvis vi ønsker at finde arealet for en funktions graf og x-aksen, hvor grafen skærer x-aksen, som den gør i figur 5, så skal vi først bestemme skæringen mellem x-aksen, da vi ellers ville få et forkert resultat.
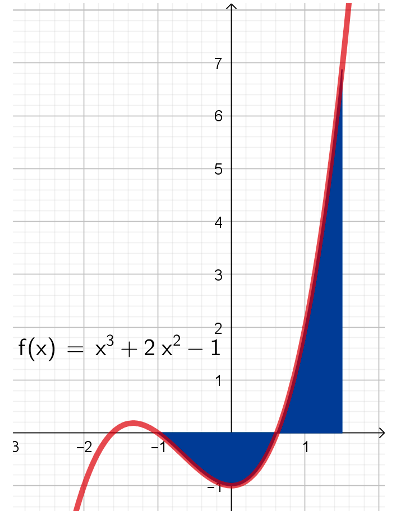
Figur 5: Areal af en funktion, som skærer x-aksen
Vi kan let beregne skæringen mellem x-aksen, ved at sætte funktionen lig med 0:
⇕ The equation is solved for x by WordMat.
Hvis vi nu ønsker at bestemme arealet af funktionen fra [-1;1.5], ved vi, at vi skal dele funktionen op i [-1;0.618] og [0.618;1.5].
Herunder beregner vi nu arealet vha. WordMat:
Vi tager den numeriske værdi af resultatet, da vi ikke kan have et negativt areal
Nu lægger vi de 2 arealer sammen:
Vi kan nu bestemme arealet til 3,45
Areal mellem 2 grafer
Når vi ønsker at finde arealet mellem 2 grafer, skal du starte med at undersøge, hvilken der ligger øverst. Her kan du nemt bare indtegne dem i et tegneprogram, som fx GeoGebra.
Figur 6: Areal mellem 2 grafer
I figur 6, er det muligt at se, at det er den blå graf der ligger øverst, og der bliver dannet et areal mellem den blå og grønne, hvilket er afgrænset mellem a og b.
Når vi nu vil finde arealet, starter vi med at finde arealet, kun for den blå graf, og ned til x-aksen, efterfulgt af den grønne graf, og ned til x-aksen, og trækker derefter de 2 arealer fra hinanden. Se figur 7 & 8.
Figur 7: Areal for den blå graf
Figur 8: Areal for den grønne graf
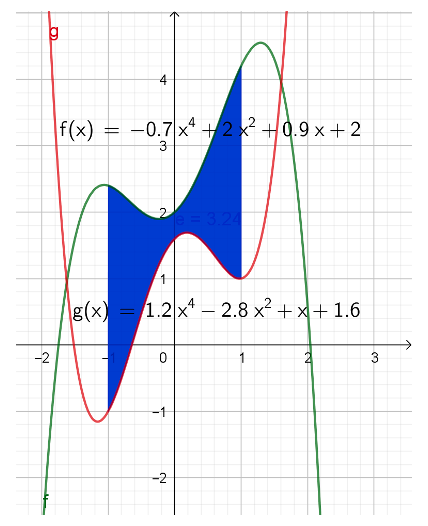
Vi vil nu lave et regneeksempel, hvor vi finder arealet mellem 2 grafer:
For at finde arealet mellem 2 grafer, kan vi også bruge formel 154, som lyder
hvor
ligger over
Vi kigger på de 2 funktioner:
Og vi bestemmer a = -1 og b = 1
Vi har nu bestemt arealet til 3,24
Her finder du formelsamlingen, som jeg flere gange refererer til i artiklen.
Held og lykke med integralregningen!